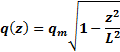Расчет САХ. Второе приближение

Юрий Арзуманян

(yuri_la)

Данная статья является продолжением темы, начатой здесь. Будем считать, что та статья является как бы первой частью материала, и так я на нее и буду ссылаться, чтобы каждый раз не приводить здесь ее полное название.

Так вот, в первой части я перечислил те основные допущения, которые положены в основу расчета крыла. Одним из таких существенных допущений является предположение, что аэродинамическая нагрузка распределена по всей консоли равномерно вдоль ее размаха и вдоль хорды. В то же время из теории и аэродинамических продувок мы знаем, что это не так. И если распределение нагрузки вдоль хорды крыла сильно зависит от профиля, то и теория, и практика показывают, что для простой формы крыла в плане профиль (эпюра) аэродинамической нагрузки вдоль размаха приближается к эллиптической кривой (например: Г. Глауэрт, Основы теории крыльев и винта, ГНТУ, 1931, стр. 113).

Таким образом, приняв допущение о равномерном распределении аэродинамической нагрузки q по крылу (здесь и далее все обозначения соответствуют таковым в первой части статьи) мы как бы предположили, что величина q является в действительности некоторой осредненной величиной. То есть имеет место предположение, что

Отсюда следует, что если на самом деле распределение аэродинамической нагрузки по размаху соответствует эллиптической кривой, то необходимо вывести соотношение, определяющее эквивалентность этих нагрузок. А эквивалентными они должны быть потому, что, в конечном счете, в равновесном горизонтальном полете подъемная сила крыла уравновешивает вес модели G. Соответственно одна консоль несет половину веса. И не важно, как распределена аэродинамическая нагрузка вдоль размаха консоли, но если помножить осредненную (среднеинтегральную) нагрузку на площадь консоли, то подъемная сила, ею создаваемая, должна быть как раз равна половине веса модели. То есть при площади консоли имеем:

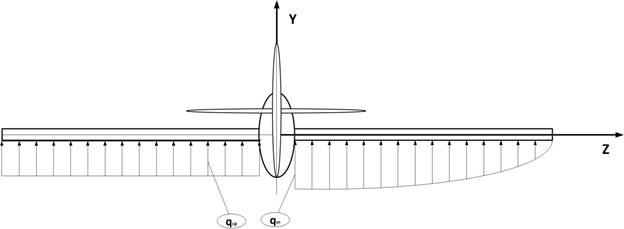
А если изобразить осредненную нагрузку на одну консоль и более близкую к действительности нагрузку с эллиптическим распределением на другую консоль, как на Рис. 1 ниже, то должна сохраняться эквивалентность нагружения, так как имеет место равновесие вокруг продольной оси модели X. Нагрузка на центральную часть крыла, затененную фюзеляжем, здесь не показана просто из-за удобства изображения, хотя по ГОСТу она входит в площадь крыла и во всех расчетах предполагается, что корневая нервюра находится в вертикальной плоскости симметрии самолета.

Рис. 1. Эквивалентное нагружение консолей крыла распределенными нагрузками

Такая эквивалентность может быть обеспечена, если площади эпюр нагружения равны.

В правой части этого выражения записана площадь четвертинки эллипса. Отсюда:

А вот для расчета приравниванием площадей эпюр нагружения не обойтись, поскольку на разном плече действует разная нагрузка, и площадь, с которой она «собрана», тоже может меняться по размаху в зависимости от формы крыла в плане. Поэтому, как и ранее, мы заменим на одной консоли распределенную нагрузку эквивалентной сосредоточенной равнодействующей силой , приложенной на неизвестном нам пока плече

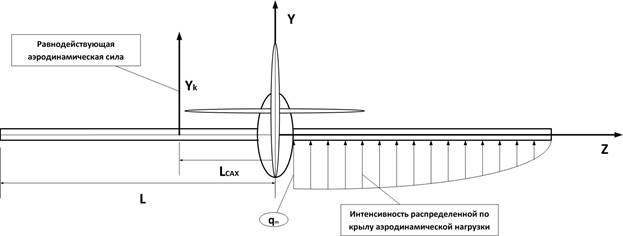
Рис. 2. Эквивалентное нагружение консолей крыла сосредоточенной и распределенной нагрузками

Таким образом, момент силы на плече на левой консоли должен быть уравновешен моментом от распределенной нагрузки на правой консоли. То есть для левой консоли:

Или

Для правой консоли будем иметь интеграл вида

Здесь – текущее значение распределенной нагрузки, а – текущее значение хорды крыла. Для эллиптического профиля эпюры распределенной нагрузки получим из уравнения эллипса следующее выражение для .

Возьмем трапециевидное в плане крыло, как наиболее распространенное. Рассмотрение этого примера будет достаточно для получения сравнительных результатов по двум подходам к расчету . Для такого крыла текущее значение хорды крыла запишется следующим образом:

Далее нам будет удобно перейти к относительным координатам.

Полуразмах тогда будет вынесен за знак интеграла, а пределы интегрирования будут находиться в интервале

Подставляя полученные выражения в уравнение для момента, получим:

Вычисление интеграла я приводить не буду, желающие могут проделать это самостоятельно. Результатом интегрирования будет следующее выражение:

Приравнивая моменты для левой и правой консоли, получим выражение для . При этом мы можем сразу использовать выражение для площади трапеции, поскольку оно известно. В итоге имеем следующую формулу:

Напомню, что при классическом методе расчета эта формула имеет такой вид:

Формула для вычисления собственно трапециевидного крыла не зависит от способа вычисления . Будь то классический метод, или предложенный здесь уточненный метод второго приближения.

Как можно видеть из сравнения двух формул для , уточненная формула не намного сложнее классической и ее вполне можно завести в модельный калькулятор. Однако прежде чем это сделать, необходимо выполнить проверку полученных результатов, а потом оценить разницу в полученных результатах с классическим методом, и решить, стоит ли игра свеч.

Посмотрим для начала, что получится для прямоугольного крыла. Понятно, что в этом случае поскольку хорда прямоугольного крыла постоянна по размаху А вот будет отличаться и составит не 0,5 то есть не центр прямоугольного крыла, что естественно, а величину 0,424 Это значение 0,424 мы с вами уже встречали в первой части статьи. И там оно относилось к эллиптического крыла при равномерном распределении аэродинамической нагрузки. Поэтому естественно, что здесь мы получили то же значение при эллиптическом законе распределения аэродинамической нагрузки, но для прямоугольного крыла. Просто поменялись местами форма крыла и форма нагрузки.

Что это означает физически? Это означает, что точка приложения равнодействующей аэродинамической силы для прямоугольной консоли крыла находится не в ее геометрическом центре, а ближе к фюзеляжу: 0,424 против 0,5 полуразмаха. Практической значимости для моделиста от этого никакой, мы просто убедились в логичности результата. А вот для трапециевидного крыла это уже некоторым образом скажется на результатах при определении центровки модели.

Рассмотрим конкретный пример. Возьмем трапециевидное крыло со следующими размерами:

Примем для простоты, что у него стреловидная передняя кромка, а задняя прямая. Посмотрим, где будет находиться ЦТ модели, если задаться центровкой 30% . Отсчет координаты центра тяжести будем проводить от носика корневой нервюры. Используя полученные формулы, проведем вычисления. Результат в Таблице 1. Все размеры в миллиметрах.

Таблица 1

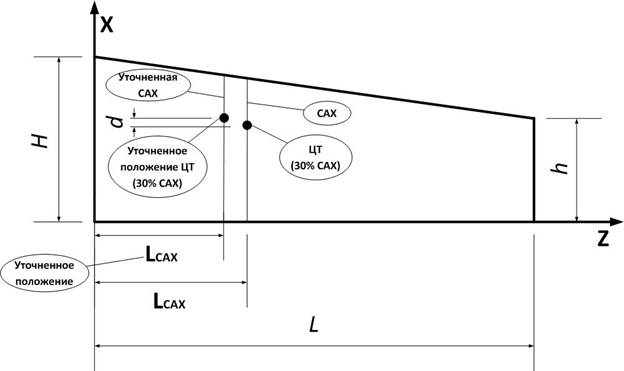
Для наглядности результаты расчетов отображены на Рис. 3.

Рис. 3. Положение ЦТ модели, рассчитанное разными методами для 30%

Как мы видим из полученных результатов, положение ЦТ по уточненной формуле должно быть сдвинуто вперед. Сдвиг центровки на Рис. 3 обозначен буквой d. И этот сдвиг составляет всего пару миллиметров. Стоит отметить, что если консоль будет не сужающейся, а расширяющейся, то центровка сдвинется назад, что логично.

Какие можно сделать выводы из полученных результатов?

Самый главный вывод заключается в том, что разница в положении ЦТ, полученном по расчету классическим методом, и по уточненной формуле, незначительна и составляет менее двух процентов величины И мы, таким образом, убедились в том, что допущение о равномерности распределения аэродинамической нагрузки вдоль размаха крыла дает вполне удовлетворительную точность. Те же моделисты, которые считают, что лучше отбросить и эту незначительную погрешность, теперь имеют более точную формулу для расчета и могут ею воспользоваться. Возможно, для больших моделей повышенная точность и будет необходима.

Чтобы закрыть тему, мне осталось рассказать о расчете секционного крыла. Об этом в следующий раз…