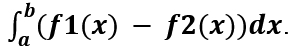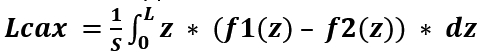| И ещё раз о средней аэродинамической хорде (САХ) |
| Изготовление авиамоделей - Разработка авиамоделей | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Автор: AndreyS | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
И ещё раз о средней аэродинамической хорде (САХ) AndreyS Человек делает свой выбор, даже если ему очевидно, что он ошибается. А.Перес-Реверте Прикидывая весовую компоновку легкой “прогулочной“ авиамодели с толкающим винтом (не люблю жаргонизмов от доморощенных космополитов: паркфлаер, пушер, рудер и т.д.), столкнулся с необходимостью вычисления средней аэродинамической хорды (далее – САХ) крыла будущего аэроплана. Так как крыло набрасывалось в творческом “запале“, то его кромки (и передняя и задняя) получились сильно криволинейными. По этой причине использование обычных методов расчета САХ не представлялось возможным.
“Великий и ужасный гугл“ привел меня к изумительной статье Юрия Арзуманяна “Расчет САХ крыла с криволинейным контуром“ (http://rc-aviation.ru/flamingo/1433-raschet-krila). Всегда завидовал (по-доброму) таким людям: просто, доходчиво, тут интегрируем, тут сокращаем, рутинную работу не показываем, чтобы не утомить, и вот вам, господа, готовый инструмент – пользуйтесь! За всем этим, конечно, стоит труд ума, эрудиция, знания. Автор упомянутой выше статьи предложил читателям попробовать другие методы аппроксимации, чем с использованием кривых Безье, однако предупредил о некоторых трудностях на этом пути: “сильного искажения контура крыла при определенном сочетании исходных данных, либо из-за своей громоздкости и вычислительной трудоемкости.“
И вот, воодушевленный прочитанной статьей и ведомый своей врожденной вредностью, я пустился по трудному, но интересному пути (своему пути) вычисления САХ. План мой был достаточно прост: 1. В качестве исходных данных взять расчетное крыло из статьи уважаемого Ю.Арзуманяна, снять координаты нескольких точек на криволинейных кромках крыла. 2. Используя координаты выбранных точек, найти интерполирующие функции, описывающие кромки крыла. 3. Построить графики интерполирующих функций и визуально сравнить совпадение построенного графика с расчетной консолью в плане. 4. Интегрированием найденных функций найти искомые величины: площади расчетного крыла, плеча САХ и, собственно, САХ. 5. Сравнить полученные результаты с первоисточником, оценить право полученной методики “на жизнь.“ Инструменты. Несмотря на долгое и мучительное знакомство с высшей математикой в трех неплохо законченных мною ВУЗ-ах, близких отношений у меня с ней (математикой) не случилось, поэтому “рукопашные“ численные методы решения данной задачи были сразу исключены. Посему в качестве инструмента был выбран ПК (не все же время ему зависать в социальных сетях). Вернее, в качестве инструмента был выбран язык программирования Python () в виде дистрибутива Anaconda (). Обосную данный выбор. Дистрибутив свободный, мощный, хорошо документирован, устанавливается на все распространенные операционные системы, несложен для освоения. Основное отличие Anaconda от Pythonв том, что в Anaconda уже установлены дополнительные библиотеки функций, которые сильно облегчают жизнь при выполнении расчетов. Немного теории. Снять с наброска (чертежа) координаты точек на кромках крыла не cоставляет большого труда.Большинство моих знакомых, даже владея серьезными программными системами автоматического проектирования, каждый творческий путь начинают на масштабно-координатной чертёжной бумаге («миллиметровке» в простонародье). С «миллиметровки» снимать координаты точек вовсе не обременительно.
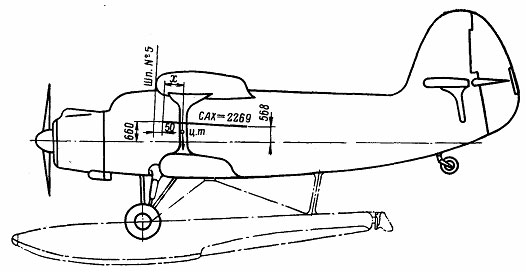
Рис.1. Снятие координат точек на кромках расчетного крыла (расчетное крыло из статьи Ю.Арзуманяна). Полученные координаты точек удобно заносить в табличку:
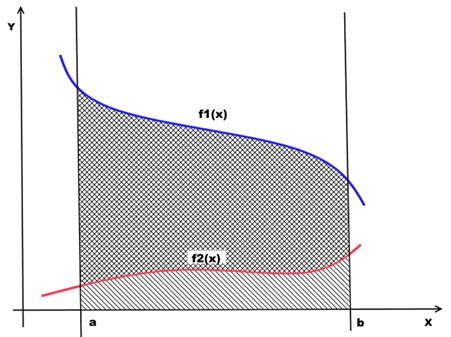
Табл. 1. Образец таблицы для регистрации координат выбранных точек на кромках расчетного крыла. Теперь надо найти такую функцию, график которой бы максимально приближался к конфигурации кромок нашего крыла. Это приближение называется аппроксимацией. Аппроксимация, или приближение – это математический метод, состоящий в замене одних математических объектов (в нашем случае координат точек) другими (найденными функциями). Нам, наверное, более интересна интерполяция. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных. Интерполяцию будем выполнять кубическими сплайнами. В переводе spline означает “гибкая линейка, рейка“. График интерполирующей функции при этом виде интерполяции можно уподобить кривой, по которой изгибается гибкая линейка, закрепленная в наших узловых точках. По-умному сплайном называется кусочно-полиномиальная функция, определенная на отрезке. Геометрически это значит, что нужно найти интерполирующую функцию, проходящую через все заданные точки. В случае интерполяции сплайном кривая F(z) состоит из кусочков, а именно, на каждом из отрезков [zi-1; zi] найденная функция является кубическим полиномом Fi(z) = ai+ bi(z-zi) + ci(z-zi)2 + di(z-zi)3 Допустим, что мы нашли интерполяционные функции, описывающие наши кромки расчетного крыла. Что дальше? Из курса математического анализа известно, что если на отрезке [a, b] некоторая непрерывная функция f1(x)больше либо равна некоторой непрерывной функции f2(x), то площадь фигуры, ограниченной графиками данных функций и прямыми x = a, x = b, можно найти интегрированием по формуле:
С точки зрения геометрии определенный интеграл – это площадь.
Рис. 2. Нахождение площади фигуры, ограниченной функциями f1(x), f2(x), x=a, x=b. Таким образом, зная функции, описывающие кромки крыла, можно вычислить площадь консоли крыла, проинтегрировав разность этих функций на интервале от корневой хорды до концевой. Рассмотрим наши найденные интерполирующие функции (практически – консоль крыла в плане) в прямоугольной системе координат.
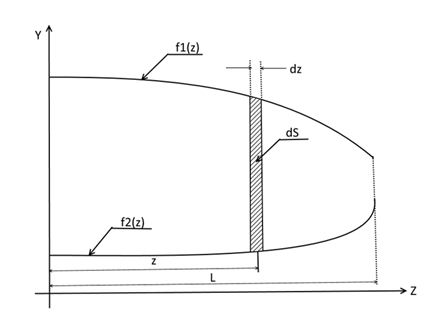
Рис. 3. Консоль крыла в плане в прямоугольной системе координат. Где: L – полуразмах крыла; z – координата элементарной площадки; dS – площадь элементарной площадки; dz – основание элементарной площадки; f1(z), f2(z) – графики интерполирующих функций. Очевидно, что длина местной хорды будет вычислена, как: f1(z) – f2(z). Тогда статический момент площади запишется как: z * (f1(z) – f2(z)) * dz. Отсюда уравнение равновесия можно записать так:
где Lcax - плечо САХ; L – полуразмах крыла. И, завершая, находим величину САХ: CAX = f1(Lcax) – f2(Lcax). Ну, и наконец-то к практике. Cнимем координаты точек с кромок расчетного крыла из статьи Ю.Арзуманяна. Занесём снятые координаты выбранных точек в таблицу:
Табл. 2. Координаты выбранных точек на кромках расчетного крыла. Приступим к “таинству“ программирования. Весь код (если это можно назвать таким высоким словом) я “ваял“ в среде разработки Spyder, которая устанавливается вместе с Anaconda. Вывод результатов происходит там же, "великий и могучий" присутствует и всё интуитивно понятно. Всего-то в этом коде пару десятков строчек (если выбросить комментарии). Пишем (или загружаем) эти строчки в среде программирования Spyder, читаем комментарии (или не читаем) и запускаем программу на выполнение. # -*- coding: utf-8 -*- # программа для расчета средней аэродинамической хорды крыла # Fri Feb 24 11:28:59 2017.
Этот e-mail адрес защищен от спам-ботов, для его просмотра у Вас должен быть включен Javascript
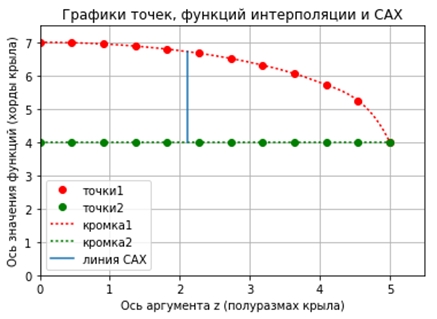
# импортируем необходимые библиотеки дополнительных функций import numpy as np import matplotlib.pyplot as plt from scipy.interpolate import interp1d import scipy.integrate as fint # создаем массивы данных с данными точек снятых с консоли крыла # массив z - аргумент функции, от корневой хорды крыла к концевой по оси Z z = np.array([0.0, 0.5, 1.0 ,1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 4.75, 5.0]) yup = np.array([7.0, 6.966, 6.853, 6.761, 6.653, 6.499, 6.284, 6.057, 5.739, 5.421, 5.199, 5.0]) ydo = np.array([1.0, 1.0, 1.017, 1.063, 1.153, 1.25, 1.41, 1.597, 1.909, 2.369, 2.767, 4.0]) # определяем начальные параметры расчета: полуразмах, корневую хорду крыла zmax = z.max() hmax = yup.max() # ищем интерполирующие функции по заданным точкам f1 = interp1d(z, yup, kind='cubic') f2 = interp1d(z, ydo, kind='cubic') # создание массива для новых значений z интерполирующей функции в диапазоне # аргумента от корневой хорды к концевой на 200-ти участках znew = np.linspace(0.0, zmax, 500) # вычисляем значение интерполирующих функции для новых значений аргумента z yupnew = f1(znew) ydonew = f2(znew) # вычисляем массив произведения новых значений аргументов и разницы значений # функций dnew = znew*(yupnew-ydonew) # ищем интерполирующую функцию для произведения новых значений аргументов # и и разницы значений функций f3 = interp1d(znew, dnew, kind='cubic') # интегрируем интерполирующие функцию по заданным точкам на интервале z # - получаем площадь расчетной секции крыла Sw1, err = fint.quad(f1, 0.0, zmax) Sw2, err = fint.quad(f2, 0.0, zmax) Sw = Sw1 - Sw2 # интегрируем статический момент площади L, err = fint.quad(f3, 0.0, zmax) # вычисляем плечо САХ Lcax = L/Sw # вычисляем САХ CAX = f1(Lcax)-f2(Lcax) # задаем границы построения графика plt.axis([0.0, zmax+0.5, 0.0, hmax+0.5]) # рисуем график снятых точек и интерполирующих функций plt.plot(z, yup, 'ro', z, ydo, 'go', znew, yupnew, 'r:', znew, ydonew, 'g:') # рисуем линию САХ plt.plot([Lcax, Lcax], [f2(Lcax), f1(Lcax)]) # подписываем оси и "обзываем" график plt.xlabel('Ось аргумента z (полуразмах крыла)') plt.ylabel('Ось значения функций (хорды крыла)') plt.title('Графики точек, функций интерполяции и САХ') # выводим легенду графиков plt.legend(['точки1', 'точки2', 'кромка1', 'кромка2', 'линия САХ'], loc='best') # выводим сетку графика plt.grid(True) # показываем график plt.show() # выводим результаты расчета print ('Площадь секции крыла, кв.дм.', Sw) print ('Плечо САХ', Lcax) print ('САХ', CAX) Рис.4. Текст программы интерполяции и расчета по табличным данным выбранных точек. Получаем такой результат:
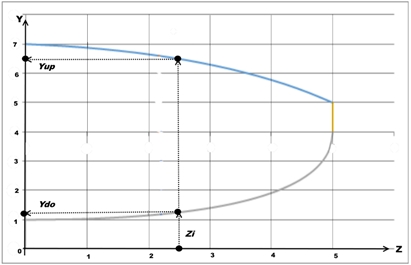
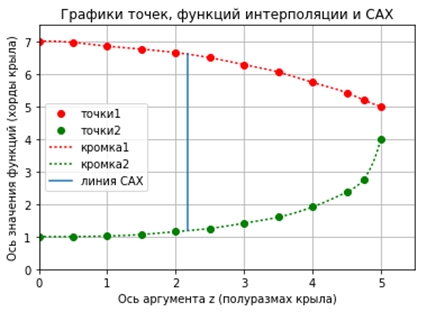
Площадь консоли крыла, кв.дм. 24.159456744034564 Плечо САХ 2.1773029967769446 САХ 5.42179302353 Рис.5. Результат выполнения программы интерполяции по табличным данным выбранных точек и расчета. Сравниваем построенный график с конфигурацией кромок расчетного крыла - терпимо. Двигаемся дальше. Сравниваем полученные результаты с результатами, опубликованными в исходном примере.
Табл. 3. Сравнение результатов исходного и выполненного расчета. Разница в площади – 0,015 кв.дм,в плече САХ – 0,47мм, что приемлемо, а вот длина САХ отличается на 17 мм, это явно многовато, даже для таких размеров консоли крыла. Чтобы развеять сомнения в пригодности данного метода вычисления САХ, была написана программа для обсчета эллипсовидного крыла. Точки на кромке крыла были вычислены по каноническому уравнению эллипса х2/а2+ y2/b2=1 (a и b – полуоси эллипса) с частотой выборки данных точек как в предыдущем расчете. После расчета получен результат, который будем сравнивать с результатом расчетов по формулам для эллипсовидного крыла, приведенных в статье Ю.Арзуманяна. Получаем такой результат:
РАСЧЕТ ПО МЕТОДИКЕ Площадь консоли крыла, кв.дм. 11.733968714326277 Плечо САХ 2.1109512756563924 САХ 2.71949454257 РАСЧЕТ ПО ФОРМУЛАМ площадь четверти эллипса, кв.дм. 11.780972450961723 плечо САХ по формуле 2.1220659078919377 САХ по формуле 2.71640590887 Сравниваем полученные результаты с результатами расчетов по формулам.
Табл. 3. Сравнение результатов полученного расчета с результатом расчетов по формулам Анализ разницы результатов показывает, что: разница в площади – 0,05 кв.дм, остальные параметры от 0,31 до 1,1мм, что весьма приемлемо, по моему скромному мнению, для вычисления САХ консоли. Выводы: 1. Язык Python (в виде дистрибутива Anaconda), как высокоуровневый язык программирования общего назначения, очень удобен и несложен для освоения и пригоден для быстрого написания несложных программ в помощь моделисту. 2. Метод интерполяции кубическими сплайнами по снятым точкам с криволинейных кромок крыла, с дальнейшим интегрированием найденных интерполирующих функций дает приемлемую точность вычисления средней аэродинамической хорды для расчетов крыла модели и имеет право на употребление. Список использованной литературы: 1. “Расчет САХ крыла с криволинейным контуром“, Юрий Арзуманян (yuri_la), http://rc-aviation.ru/flamingo/1433-raschet-krila. 2. “Основы численных методов“, учебное пособие для студентов факультета физики РГПУ им. А.И. Герцена, . 3. ГОСТ 22833-77 “Характеристики самолета геометрические. Термины, определения и буквенные обозначения.“ 4. “Язык программирования Python 3 для начинающих и чайников.“, . 5. “Numpy and Scipy Documentation.“, , (англ.). Послесловие: Возможно, что настоящие математики и программисты посмеются над моими “творческими потугами“, но я получил нужный мне инструмент расчета, причём, без особых трудозатрат. Ещё в активе - разминка ржавых мозгов. В дальнейшем, планирую написать программулину, считывающую точки на криволинейных кромках прямо с рисунка (чертежа). Но об этом – позже. |
