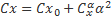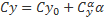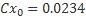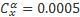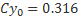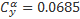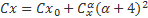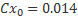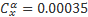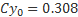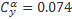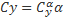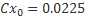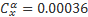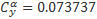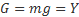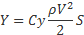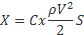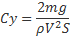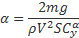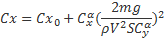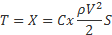| Сравнительный анализ профилей крыла для скоростных маневренных моделей |
| Изготовление авиамоделей - Разработка авиамоделей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Автор: Administrator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Сравнительный анализ профилей крыла для скоростных маневренных моделей Юрий Арзуманян (yuri_la) Данная статья является обобщением обсуждения этой темы на форуме rc-aviation. Речь там шла конкретно о моделях воздушного боя, и, в частности, такого типа, как на Рис. 1 ниже.
Рис. 1. Бойцовка SB-7AS от клуба Alisa Air Я намеренно не упомянул это в заголовке статьи, поскольку примененный ниже подход применим не только к моделям воздушного боя. Более того, этот подход был впервые предложен еще на заре авиации одним из отцов-основателей современной аэродинамики нашим великим ученым Николаем Егоровичем Жуковским. С тех пор предложенный им метод так и называют методом потребных тяг Н.Е. Жуковского. Чтобы не повторять то, что обсуждалось в форуме, замечу, что вопрос об использовании вместо относительного толстого симметричного профиля более тонкого и, в особенности, несимметричного профиля для бойцовок, возникает с определенной периодичностью. Не случайно говорят, что все новое – это хорошо забытое старое. Ведь к симметричному относительно толстому профилю ведущие бойцы пришли неспроста. За этим стоят годы проб, ошибок, нахождения компромиссов и накопления опыта. Я не буду углубляться в тему воздушного боя, поскольку последний раз управлял кордовой бойцовкой еще в пионерском детстве, и не считаю себя в этом деле экспертом. Для этого лучше внимательно проштудировать соответствующие разделы форумов, поскольку там отмечаются настоящие спортсмены, а не просто любители. Скажу только, что основные аргументы в пользу перехода на более тонкий несимметричный, а то и вообще плоско-выпуклый профиль, обычно сводятся к следующим:
1) Более низкое лобовое сопротивление модели, отсюда более высокая достижимая скорость полета. 2) Время прямого полета в ходе боя в среднем больше времени полета в инверте, поэтому прямой полет более важен. 3) Меньший вес и стоимость изготовления модели. Есть и другие предполагаемые достоинства, но они спорны, и упоминать я их не буду. А основным недостатком при этом считается ухудшение качества обратного пилотажа (в перевернутом полете). Итак, давайте приступим к сравнению профилей. Казалось бы, ожидаемый результат анализа очевиден. Действительно, более тонкий профиль имеет меньшее лобовое сопротивление. Значит, скорость полета будет больше, и с этим не поспоришь! Но... давайте займемся расчетами и посмотрим насколько это справедливо. Для получения числовых результатов надо отталкиваться от конкретных характеристик. Поэтому примем следующие исходные данные для модели с фото. Характеристики планера бойцовки на Рис. 1: Размах крыла - 1000 мм Площадь крыла – 20.8 кв. дм. Взлетная масса модели - 475 грамм Расчетная скорость полета - 32 м/с (это всего лишь некоторая опорная величина, дальше в расчетах скоростью будем варьировать) Исходный профиль - симметричный 15% (NACA 0015 – близок к исходному) Мотор- Eurgle RC Plane 1580kv D2810 Brushless Outrunner Back Mounting Motor (300W) Батарея - 2200мА 3S 25С Регулятор на 40А Статика на стенде: Винт - МА 8х5 Ток - 26А Мощность - 270W Тяга - 980 гр. Для сравнения возьмем два профиля ЦАГИ. Первый – чисто плоско-выпуклый профиль ЦАГИ-719, относительная толщина примерно 10%. Второй профиль тоже ЦАГИ, только он со скругленной передней кромкой. Это ЦАГИ-831. Наш анализ серьезно облегчается тем, что мы рассматриваем летающее крыло без выраженного фюзеляжа. Поэтому в общей величине аэродинамического сопротивления это можно учесть небольшим поправочным коэффициентом, но на СРАВНИТЕЛЬНЫЕ результаты это не сильно повлияет. Чтобы провести соответствующие расчеты надо знать аэродинамические характеристики каждого профиля. Начнем с плоско-выпуклого. Таблица 1. Геометрия профиля ЦАГИ-719.
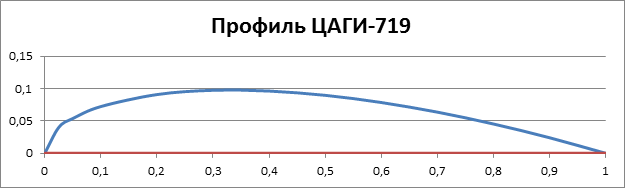
Вот так он выглядит:
Рис. 2. Контур профиля ЦАГИ-719
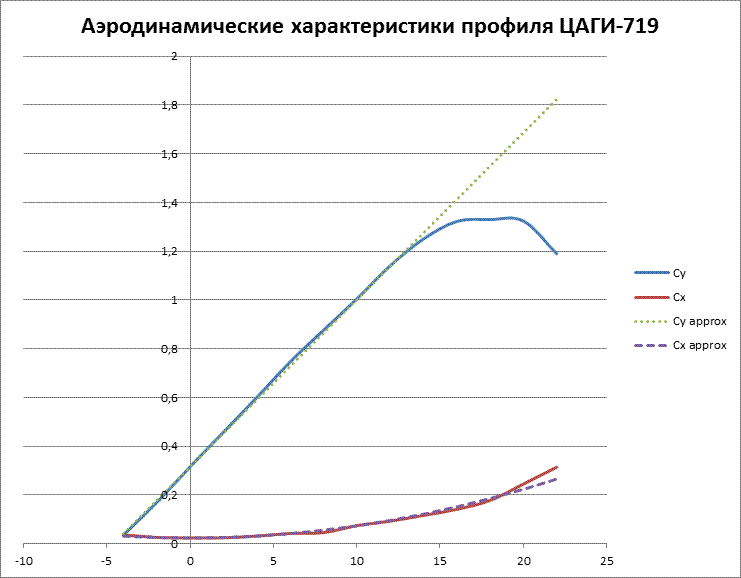
А его характеристики в таблице ниже. Таблица 2. Аэродинамические характеристики профиля ЦАГИ-719
В расчетах можно пользоваться табличными данными. Только в этом случае придется промежуточные значения интерполировать, а это влечет за собой громоздкие вычисления и вообще не очень удобно. Чтобы этого избежать, я пользуюсь тем, что нас интересует ограниченная область углов атаки, где табличные данные легко аппроксимировать аналитической формулой. Я вывел такие аппроксимирующие формулы для Сх и Су:
Здесь ? - угол атаки в градусах.
и
Смотрим, насколько удачна наша аппроксимация.
Рис. 3. Аппроксимация аэродинамических характеристик профиля ЦАГИ-719 Из графиков видно, что в зоне малых углов атаки приближение аналитическими формулами вполне удовлетворительное. Далее мы сделаем то же самое для второго плоско-выпуклого профиля, но со скругленной передней кромкой. Он чуть толще – 11%. Таблица 3. Геометрия профиля ЦАГИ-831
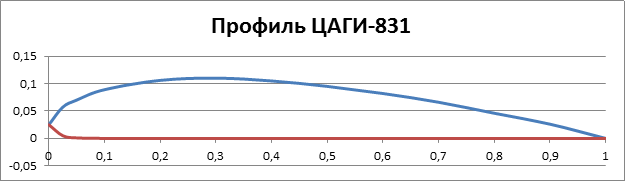
Вот так он выглядит:
Рис. 4. Контур профиля ЦАГИ-831 Аэродинамические характеристики в таблице ниже. Таблица 4. Аэродинамические характеристики профиля ЦАГИ-831
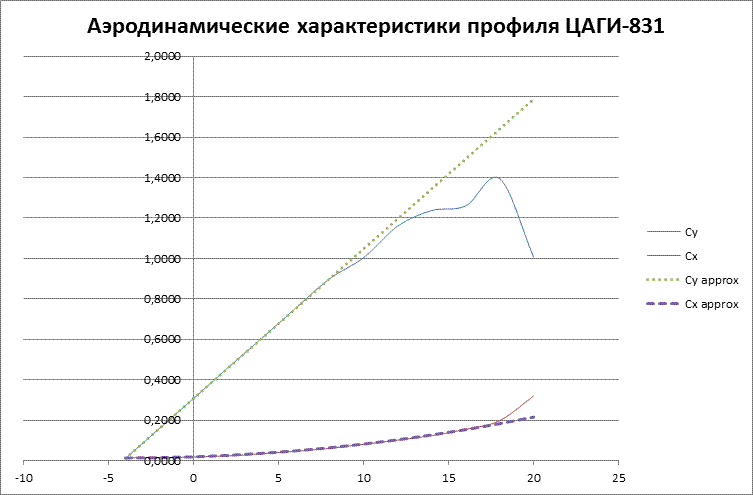
Для этого профиля выведены такие аппроксимирующие формулы для Сх и Су:
где
и
Так выглядят графики аэродинамических характеристик для этого профиля.
Рис. 5. Аппроксимация аэродинамических характеристик профиля ЦАГИ-831 Нам осталось привести характеристики симметричного профиля. Вот они: Таблица 5. Геометрия профиля NACA-0015
Так выглядит симметричный профиль.
Рис. 6. Контур профиля NACA-0015
Таблица 6. Аэродинамические характеристики профиля NACA-0015
Здесь такие аппроксимирующие формулы для Сх и Су:
где
и
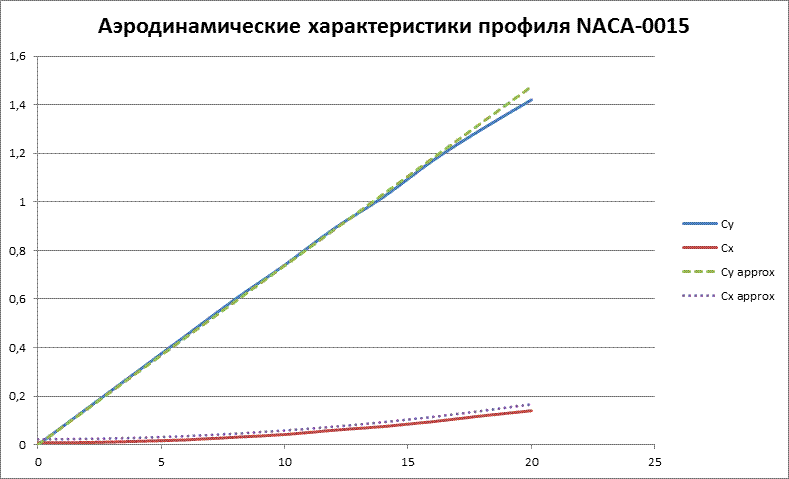
Так выглядят графики аэродинамических характеристик для этого профиля.
Рис. 7. Аппроксимация аэродинамических характеристик профиля NACA-0015 Теперь у нас есть все данные для проведения сравнительных расчетов. Рассмотрим прямолинейный установившийся горизонтальный полет с постоянной скоростью. Поскольку в таком полете подъемная сила уравновешивает вес модели, то для каждой скорости можно найти требуемый балансировочный угол атаки. Для этого мы зададимся некоторым диапазоном скоростей полета модели. Для каждой скорости полета вычислим лобовое сопротивление. Поскольку в полете с постоянной скоростью тяга уравновешивает лобовое сопротивление, то, имея угол атаки, мы это сопротивление вычислим, и получим потребную тягу для полета на этой скорости. То есть имеют место равенства:
Выражения для подъемной силы и лобового сопротивления такие:
Здесь: g – ускорение свободного падения m – масса модели G – вес модели Y – подъемная сила T – сила тяги X – лобовое сопротивление S – площадь крыла V – скорость полета
Последовательность расчетов следующая. Задаемся скоростью полета в интересующем нас диапазоне. Тогда из выражения для Y можно вычислить потребное значение коэффициента подъемной силы для установившегося полета на этой скорости.
Имея для каждого профиля аппроксимирующие формулы, мы по значению Cy вычислим потребное значение балансировочного угла атаки. Например, из этой формулы для NACA-0015.
получим
Подставив его в выражение для Cx,
и далее в формулу для лобового сопротивления
получим величину лобового сопротивления, равного потребной тяге для данной скорости полета. Это простая арифметика и я не буду здесь приводить пример числового расчета, а сразу приведу результат в виде таблицы и графика потребных тяг для всех трех профилей. Таблица 7. Зависимость потребной тяги от скорости полета
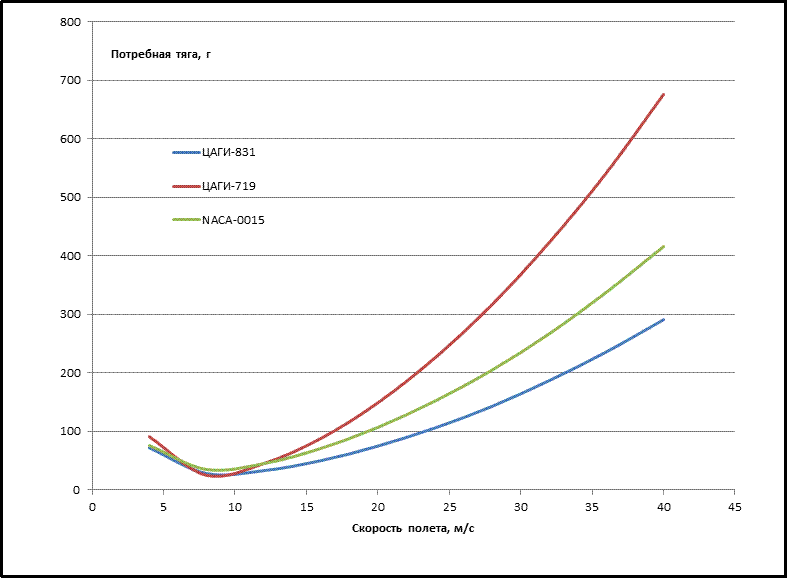
Из этой таблички видно, что для опорной скорости полета 32 м/с наименьшая потребная тяга у профиля ЦАГИ-831. Затем идет симметричный профиль NACA-0015, и хуже всего результаты у профиля ЦАГИ-719. Наглядно все это продемонстрировано на графике.
Рис. 8. График потребных тяг сравниваемых профилей в зависимости от скорости полета В общем, предварительные результаты расчетов катастрофические для профиля ЦАГИ-719. Получается, что этот профиль хорошо летит в диапазоне скоростей полета 6-10 м/с. Такой полет происходит на околонулевом угле атаки при скоростях менее 40 км в час. Для полета на более высоких скоростях, в частности для заданной скорости 32 м/c (115 км/ч) необходимо лететь на ОТРИЦАТЕЛЬНОМ угле атаки около четырех градусов! Это чистая теория, на практике так модель лететь не будет. Ею будет практически невозможно управлять. Но вывод однозначен - этот профиль не для таких моделей. Стоит заметить, что выбранные два профиля ЦАГИ существенно отличаются скруглением носка, и теперь видно насколько это влияет на летные характеристики крыла. Я намеренно взял два таких похожих профиля, у которых только носок разный, чтобы показать это влияние. Также из таблицы можно видеть, что при одинаковой располагаемой тяге в зоне скоростей выше опорной разница в развиваемой скорости составит примерно процентов пятнадцать. То есть преимущество (в данном случае у ЦАГИ-831 по сравнению с NACA-0015) у несимметричного профиля перед симметричным есть, но небольшое! Для симметричного профиля NACA-0015 балансировочный угол на расчетной скорости 115 км в час положительный, примерно полградуса, потребная тяга на этом режиме примерно 270 грамм. Я думаю, что если и дальше исследовать вопрос, то может быть стоит посмотреть более тонкие симметричные профили. Хотя если наложено ограничение на максимальную допустимую перегрузку из условий прочности, то время установившегося виража линейно растет с увеличением скорости полета. То есть более тонкие симметричные профили приведут к росту скорости, но снижению маневренности. Дебаты на тему маневренность против скорости активно велись перед Второй Мировой Войной. Мессершмитты Me-109 против наших Чаек (И-153) и Ишачков (И-16). Скорость победила. Но в тех боях не было правил. Не было ограничения полетной зоны и т.п. Что лучше для боя радиоуправляемых моделей – не мне решать. В заключение хотел бы указать то направление, в котором было бы целесообразно продолжить теоретические изыскания, после того, как вы определились с профилем крыла. Это оптимизация винтомоторной группы (ВМГ). Мощность мотора – обороты (kv) – диаметр и шаг винта. Но это уже совсем другая тема… Здесь же я хочу выразить благодарность Геннадию Шабельскому (SURHAND) и Тарасу Кушниренко (Kushnirenko) за поддержку и практическую помощь в написании данной статьи. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||