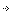САХ и геометрия авиамодели

Юрий Арзуманян

(yuri_la)

Данная статья является завершающей в «трилогии», посвященной расчету Средней Аэродинамической Хорды (САХ) крыла. Она была начата статьей «Расчет САХ крыла с криволинейным контуром» и была продолжена в статье «Расчет САХ. Второе приближение». Таким образом, я выполняю свое обещание рассказать о расчете САХ секционного крыла, данное во второй статье, и завершаю этим данную «трилогию».

Прежде чем перейти к предмету статьи стоит отметить, что расчет САХ не является для моделиста самоцелью, это скорее инструмент для определения правильной центровки модели. А если пойти еще дальше, то для самостоятельно проектируемой модели самолета такой расчет необходим для правильного выбора ее геометрии. Поэтому здесь я бы еще хотел перекинуть мостик к этой самой следующей теме, которую в рамках одной короткой статьи осветить невозможно. Эта тема особенно важна, поскольку тянет за собой устойчивость и управляемость модели хотя бы, для начала, в вертикальной плоскости (в канале тангажа), то есть в значительной мере отвечает на вопрос «как же оно полетит, то, что мы построили»?

Начнем все же с секционного крыла. Одновременно мы захватим и метод расчета САХ для крыла с поперечным углом V. Итак, возьмем для примера крыло с двойным изломом, характерное для планеров и других свободнолетающих моделей. Я изложу алгоритм расчета, и надеюсь, что читатель уже самостоятельно справится с задачей, если число секций крыла будет не две, а три или более. Например, третьей секцией консоли можно в ряде случаев считать законцовку крыла, если она достаточно выражена и имеет такие размеры, что пренебречь ею нежелательно.

Конфигурацию крыла в плане примем трапециевидной, так как такая форма является наиболее распространенной. Как быть в случае если конфигурация крыла в плане имеет криволинейный контур, мы знаем из первой статьи. Смотрим на Рис. 1.

Рис. 1. Конфигурация двухсекционного крыла с двойным поперечным изломом

Поскольку крыло не плоское, то надо вспомнить, что ГОСТ 22833-77 требует рассматривать проекцию крыла на горизонтальную плоскость. С этого и начнем. Из геометрии нам известно, что если некая прямая параллельна плоскости, то ее проекция на эту плоскость будет той же длины. Поэтому хорды секций крыла , и останутся без изменений. А вот длины секций (вдоль размаха) надо умножать на косинус угла V соответствующей секции. Тогда получим такую картинку, как на Рис. 2.

Рис. 2. Проекция консоли крыла на горизонтальную плоскость

Таким образом, вместо и мы получим и .

Соответственно надо пересчитать площади проекций для каждой секции крыла.

Общая площадь:

Далее мы должны подсчитать для каждой секции по известной нам формуле. Ранее мы убедились, что предположение о равномерном распределении аэродинамической нагрузки по размаху дает вполне удовлетворительные результаты. Поэтому здесь я буду придерживаться классического подхода. Однако нет никаких препятствий для использования и более точной формулы, выведенной во второй статье.

Итак, для первой секции:

И для второй:

Важно отметить, что полученные значения дают расстояния до САХ каждой секции от корневой нервюры этой секции. Поэтому для первой секции это расстояние от продольной оси модели, а для второй секции надо прибавить полученное значение к длине проекции этой секции. Далее необходимо найти САХ всей консоли из уравнения равновесия относительно продольной оси, как мы это делали ранее. То есть:

Теперь мы знаем на каком расстоянии от продольной оси модели находится САХ нашего секционного крыла. Но поскольку мы рассматриваем самый общий случай, то надо учитывать, что длины секций, точнее их относительные размеры, могут сильно различаться в ту или иную сторону. Поэтому надо в первую очередь сравнить полученное значение с длиной первой секции. Если оно меньше , то это означает, что САХ находится в первой секции и наоборот. В первом случае находим САХ из следующего выражения:

Если значение больше длины первой секции , то есть САХ находится во второй секции, тогда формула для ее вычисления будет такой:

После того как мы нашли нужные нам величины на проекции консоли крыла нам надо перейти к действительным размерам на реальном крыле. Величина САХ при этом будет той же, а вот для нахождения ее положения на реальной консоли надо сделать обратный пересчет по формуле:

для первой секции.

Или:

для второй.

Величина отсчитывается от корневой нервюры соответствующей секции вдоль реальной консоли крыла.

Собственно говоря, здесь уже можно поставить точку в данной теме. Но поскольку, как было сказано выше, расчет САХ не является самоцелью, то следующей задачей, которую приходится решать моделисту, является выбор правильной центровки модели. И это, пожалуй, одна из наиболее часто встречающихся проблем и авиамодельные форумы пестрят сообщениями с просьбой подсказать правильное положение ЦТ той или иной модели, и ответами тех, кто может, или считает, что может, дать свои рекомендации.

К счастью, подавляющее большинство продаваемых моделей, или тех, что моделисты строят по имеющимся чертежам, либо относятся к классической аэродинамической схеме, для которых стандартная рекомендация «установите центровку на 25-30% САХ для начала, а потом корректируйте» работает, либо имеется информация по рекомендуемой центровке для прототипа, по которому имеются эти самые чертежи.

А как быть, если прототипа нет, а моделист хочет самостоятельно спроектировать и построить модель? Например, какова должна быть площадь хвостового оперения, и каким должно быть плечо этого оперения хотя бы для самолета классической схемы? Ведь должны же быть какие-то рекомендации или формулы для расчета? Таких рекомендаций немного, но они есть. Их можно найти, скажем, здесь. Советую, правда, изучить источник, из которого взяты эти рекомендации. Он приведен в конце статьи по ссылке. Это книга Р. Вилле «Постройка летающих моделей копий». Речь идет, в частности, о приведенных в ней рекомендуемых значениях коэффициентов для относительной площади горизонтального оперения и его плеча.

Но и здесь, правда, следует сделать оговорку, что приведенными рекомендациями надо пользоваться осторожно. Так, например, в книге А. Болонкина «Теория полета летающих моделей» содержится предупреждение (стр. 278) о том, что «устойчивость модели определяется не величиной коэффициента статической устойчивости … как это утверждают многие моделисты (выделено мной – авт.)…», а другими параметрами, которые надо учитывать. В нижеприведенной формуле в числителе стоит площадь стабилизатора, а в знаменателе площадь крыла.

Книга А. Болонкина является фундаментальным трудом, который я настоятельно рекомендую проштудировать тем, кто хочет хорошо разбираться в предмете. Здесь же я пока отмечу только следующее. Весь приведенный выше материал, включая две первые статьи, дает, я надеюсь, достаточный инструмент для нахождения САХ различных конфигураций крыла модели. Далее, поскольку рекомендованную центровку принято как раз относить к САХ крыла, то для существующей модели, или модели, для которой имеется чертеж, задачу можно считать решенной. Надо просто следовать рекомендациям. Однако если вы проектируете модель с нуля, то таких конкретных рекомендаций нет. Более того, вы можете рассматривать различные понравившиеся вам конфигурации крыла и хвостового оперения в плане. Прямоугольные, трапециевидные, эллиптические и т.д. И теперь хотя бы для вычисления упомянутых коэффициентов нужны некоторые опорные значения. Например, что такое плечо горизонтального хвостового оперения? От какой точки его отсчитывать? К сожалению, в этом вопросе имеется некоторая путаница. Часто за такую величину принимают расстояние между крылом и стабилизатором, но в связи с многообразием возможных конфигураций модели и здесь не все так ясно.

Казалось бы, самое правильное обратиться к ГОСТ. Но дело в том, что и упомянутый выше ГОСТ не дает на этот вопрос однозначного ответа. В нем сказано, что плечо горизонтального хвостового оперения – это расстояние (в проекции) от заданной точки на САХ крыла обычно в диапазоне центровок самолета (выделено мной – авт.) до точки, лежащей на 25% САХ горизонтального оперения. Что значит «обычно»? И в каком таком «диапазоне»? Получается, что – может быть любым в пределах этого диапазона?!

С моей точки зрения как-то разрешить эту неопределенность можно следующим образом. Когда мы с вами рассчитывали значение , то определяли расстояние до линии приложения равнодействующей аэродинамической силы на консоли крыла от продольной оси Х. Но мы не определяли где на этой линии находится точка приложения равнодействующей силы. То есть мы не находили положение Центра Давления консоли. Иными словами мы не определяли координаты ЦД по оси Х. А чтобы ее определить, нужно, так же как мы это делали раньше, составить уравнения равновесия консоли, но не относительно продольной оси Х, а относительно поперечной оси Z.

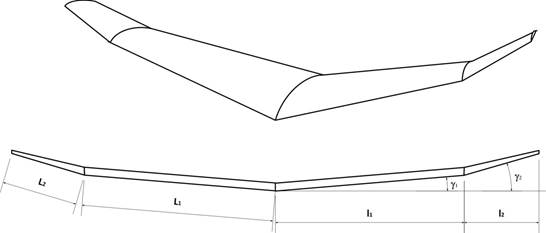
Я не буду приводить здесь все выкладки, так как эта задачка теперь уже для нас тривиальная, а сразу приведу результирующую формулу. Итак, если принять за начало отсчета носок корневой нервюры, то координата ЦД вдоль продольной оси Х для трапециевидной консоли будет равна:

Для наглядности рассматриваемая ситуация показана на Рис. 3. Там же показано, что обозначает ранее не встречавшаяся величина , задающая стреловидность по передней кромке. Обратите внимание, что положение ЦД не зависит от длины консоли, а только от значений хорд и стреловидности крыла.

Рис. 3. Определение ЦД на консоли

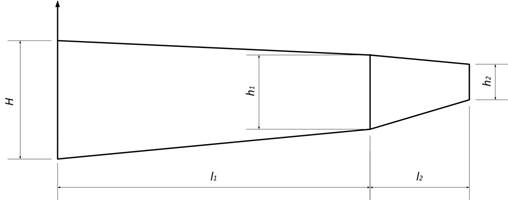
Что делать дальше? Дальше нужно по этой же формуле определить координату для хвостового горизонтального оперения, подставив соответствующие входящие в нее значения для стабилизатора. Полученное значение будет давать расстояние до ЦД стабилизатора от носика его корневой нервюры.

Вот теперь в качестве опорной величины можно принять расстояние между этими двумя центрами давления: крыла и стабилизатора. То есть, если принять за начало отсчета носик корневой нервюры крыла, и если нам известно (или мы хотим этой величиной задаться) расстояние между носиком корневой нервюры крыла и носиком корневой нервюры стабилизатора, то вычислится следующим образом:

Смотрим на Рис. 4.

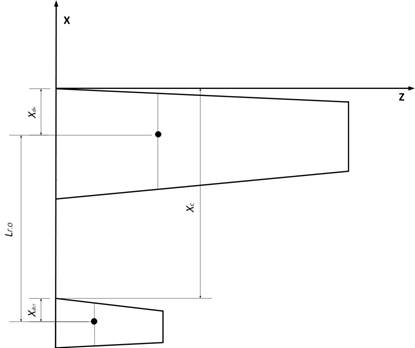
Рис. 4. Геометрия несущих плоскостей модели в плане

Как мы видим, является расстоянием между точками приложения аэродинамических сил крыла и стабилизатора, что вообще говоря и подразумевается физическим смыслом этой величины.

Нам осталось проверить полученные формулы на числовом примере. Как и в предыдущих статьях, мы возьмем консоль крыла со следующими размерами:

Стабилизатор пусть имеет следующие размеры:

Расстояние от передней кромки крыла до передней кромки стабилизатора у корневых нервюр:

Примем для простоты, что и у крыла, и у стабилизатора стреловидная передняя кромка, а задняя прямая. Посмотрим, где будет находиться ЦТ модели, если задаться центровкой 30% . Отсчет координаты центра тяжести будем проводить от носика корневой нервюры крыла. Используя полученные формулы, проведем вычисления. Результат в Таблице 1.

Таблица 1

Как видно из таблицы, значение полученное расчетом, незначительно отличается от значения, полученного согласно ГОСТ, но при этом дает более консервативную оценку. Поскольку определенная осторожность в этом вопросе не повредит, то я считаю, что предложенный метод устранения неоднозначности в определении величины вполне оправдан.

Более тщательный анализ устойчивости полета модели и выбор ее геометрии требует дополнительных усилий. Здесь без хотя бы самых грубых оценок аэродинамических характеристик крыла и хвостового оперения, углов их установок и т.п., не обойтись. Но это уже совсем другая тема…