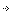| Расчет САХ крыла авиамодели с криволинейным контуром |
| Изготовление авиамоделей - Разработка авиамоделей |
| Автор: Юрий Арзуманян |
|
РАСЧЕТ САХ КРЫЛА С КРИВОЛИНЕЙНЫМ КОНТУРОМ Юрий Арзуманян (yuri_la) Прежде, чем решать задачу, надо понимать, что будешь делать с результатом. Задачу можно решать двумя путями: можно с интегралами, а можно с дробями. Результат один и тот же, но с дробями проще… Введение Задача расчета САХ (Средней Аэродинамической Хорды) крыла возникает в практике авиамоделиста довольно часто. Существует ГОСТ 22833-77, в котором дано определение САХ и приведена общая формула для ее расчета. Правда, ГОСТ не объясняет, почему используется именно эта формула, и как ею реально пользоваться. Однако, в подавляющем большинстве случаев, когда рассматривается крыло простой формы в плане, с прямыми кромками, то есть трапециевидное, треугольное и т.п., необходимости вдаваться в математику нет никакой. Когда не было компьютеров, САХ определяли графическим методом. В качестве методических пособий использовались даже специальные плакаты, которые красовались на стенах авиамодельных секций и кружков.
Рис. 1. Учебный плакат-пособие
Сейчас существуют простые модельные калькуляторы (программы), которые можно установить на компьютер, или пользоваться ими онлайн. На RC-Aviation, например, доступен такой.
В нем, правда, отсутствует возможность расчета САХ крыла с криволинейным контуром. А иногда именно это и нужно. Вот, например, популярный у начинающих «Дракоша» (в данном случае Wing Dragon 500) от Art-Tech (Рис. 2). Его крыло имеет небольшую стреловидность по передней кромке у корневой нервюры, а дальше скругление к законцовке.
Рис. 2. «Дракоша» Как рассчитать САХ для такой формы крыла? Уравнение кривой, описывающей переднюю кромку крыла неизвестно. Возможно, существуют более серьезные компьютерные программы, чем упомянутые мной простые модельные калькуляторы, которые, если есть введенное в компьютер графическое изображение контура крыла (проекции), обеспечивают такую возможность даже при отсутствии формул для кривизны кромки. Ну, а если у вас такого контура еще нет? Вы еще только прорисовываете контур крыла и хотите прикинуть разные варианты? Поэтому целью данной статьи я ставил не только вывод конечных формул для расчета САХ такого крыла, но и раскрытие общего алгоритма расчета. Иными словами, хотелось показать, КАК это делается для понимания полученного результата. Я предлагаю лишь один из возможных подходов к аппроксимации криволинейного контура с использованием кривых Безье, но этот метод не единственно возможный. Стоит заметить, что я попробовал разные методы. В частности, напрашивающийся метод с помощью сплайн-аппроксимации, с помощью степенных функций и др. Эти методы меня не устроили либо из-за сильного искажения контура крыла при определенном сочетании исходных данных, либо из-за своей громоздкости и вычислительной трудоемкости. Метод с использованием квадратичных Немного теории Средней аэродинамической хордой принято считать хорду эквивалентного прямоугольного крыла, в идеале обладающего аналогичными аэродинамическими характеристиками, как и исходное. И положение центра тяжести самолета (ЦТ) в аэродинамике и динамике полета принято отсчитывать в процентах от САХ. Это позволяет уйти от всего многообразия форм крыла в плане и привести его к «общему знаменателю». Наконец, это просто удобно в практическом плане. Итак, речь у нас идет о крыле самолета, а оно предназначено для создания подъемной силы, которая возникает за счет взаимодействия воздушного потока с крылом. Характер этого взаимодействия очень сложный, и в механизм создания подъемной силы крыла мы здесь вдаваться не будем, так же, как и не будем учитывать другие несущие элементы конструкции, хотя полученные выводы применимы и для другой несущей плоскости. Отметим только следующие моменты: - Подъемная сила крыла создается всей его поверхностью, то есть она является распределенной, а не точечной аэродинамической нагрузкой; - Распределение этой нагрузки по всей поверхности крыла неравномерно, как вдоль хорды, так и по размаху. Оно зависит от многих факторов, таких как форма крыла в плане, профиль (форма нервюр), крутка крыла, интерференция крыла и фюзеляжа, концевой вихрь, шероховатость поверхности, скорость и высота полета, угол атаки и т.д. и т.п. На деле учесть теоретически все перечисленные факторы вряд ли возможно, тем более на стадии проектирования, когда и самолета-то еще нет. Однако поскольку САХ является условной опорной величиной, то целесообразно отбросить весь этот набор искажающих картину факторов, и принять одно глобальное допущение о том, что крыло является как бы плоским, и аэродинамическая нагрузка распределена по всей его площади равномерно. Тогда вычисление САХ становится возможным в аналитическом виде, то есть с помощью формул. В механике принято в необходимых случаях заменять распределенную нагрузку равнодействующей силой, приложенной в той точке нагруженной поверхности, в которой такое воздействие точечной силы создаст эквивалентное нагружение тела. А САХ нам и нужна для того, чтобы определить то место на крыле, в котором и была бы приложена эта самая воображаемая равнодействующая аэродинамическая сила. Чтобы найти это место, нам надо вычислить расстояние до него от оси симметрии крыла (плечо САХ), и саму величину САХ, поскольку она является хордой эквивалентного прямоугольного крыла, центр давления которого (та самая равнодействующая) приложена точно в середине хорды. Вот к этому мы и приступим. Метод расчета На следующем рисунке показан вид вдоль продольной оси самолета на прямое плоское крыло. Продольная ось в системе координат самолета обозначена X, вертикальная Y, а поперечная (вдоль размаха крыла) – Z. При проведении расчетов все силы и моменты, действующие на летательный аппарат, проецируют на оси или базовые плоскости выбранной системы координат. Система координат выбирается под задачу. В нашем случае это связанная система координат. О проекциях на базовые плоскости будет сказано ниже, пока же мы рассмотрим крыло простой формы, лежащее в базовой плоскости OXZ.
Рис. 3. Нагружение крыла На правой консоли крыла показана распределенная аэродинамическая нагрузка с интенсивностью q. Размерность ее – сила, деленная на площадь, то есть давление. На левой консоли показана эквивалентная сосредоточенная сила Yk, которая приложена в точке, удаленной от оси на расстояние (плечо) Lcax. В результате эквивалентности такого нагружения крыло находится в равновесии, то есть сумма моментов относительно оси Х (начала координат) равна нулю. Тогда в левой части уравнения момент можно записать как произведение Yk на Lcax, а в правой – брать бесконечно малую элементарную площадку, умножать ее площадь dS на интенсивность нагружения q, и на расстояние от этой элементарной площадки до оси, то есть координату z. Таких элементарных площадок будет бесконечное множество, и чтобы все это не суммировать, надо взять обыкновенный интеграл по площади. Собственно говоря, именно этот интеграл и записан в определении САХ в вышеупомянутом ГОСТе. Таким образом, уравнение равновесия можно записать так:
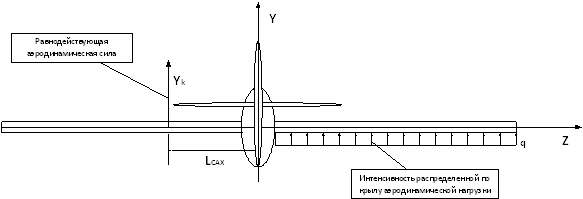
Но поскольку Yk представляет собой силу, «собранную» со всей площади консоли крыла, то получить ее можно, просто помножив интенсивность аэродинамической нагрузки q на всю площадь консоли S. Тогда q в левой и правой части уравнения сократится, и в нем останутся только геометрические параметры. В свою очередь площадь элементарной площадки dS можно вычислить, как это принято в математике, как площадь бесконечно малого элементарного прямоугольника с высотой, равной значению функции x = f(z) на координате z, умноженную на длину основания этого прямоугольника dz. Для наглядности это показано на Рис. 4.
Рис. 4. Консоль крыла в плане Тогда уравнение равновесия можно переписать так:
Здесь L – полуразмах крыла. Подынтегральное выражение называется статическим моментом площади. В этом выражении нам неизвестен вид уравнения x = f(z). Кроме того, нам неизвестна площадь консоли S. Если бы контур крыла был образован прямыми линиями, то мы бы имели простое уравнение прямой, а площадь бы вычислялась, как площадь простой геометрической фигуры (трапеция, треугольник, параллелограмм и т.п.). Тогда взятие интеграла не составляло бы труда и, соответственно, получение искомого Lcax. Отсюда следующим шагом стало бы вычисление искомого значения САХ: САХ = f(Lcax) Так вот, модельные калькуляторы САХ именно этими формулами и пользуются. Прежде чем продолжить наши выводы, я сразу эти формулы здесь и приведу, чтобы они были у вас при случае под рукой. Lcax = L[(H + 2h)/(H + h)]/3 САХ = H – (H – h)Lcax/L Если известна аналитическая формула, описывающая контур крыла, то таким способом можно вычислить САХ для более сложных крыльев в плане. Например, для эллиптического крыла (правильный эллипс, а не «примерно» эллипс).
Или приближенно Lcax = 0,212 L; САХ = 0,905 H. Кстати, на Рис. 1 крайне правое в верхнем ряду как раз показано эллиптическое крыло, и приведено значение САХ. Только там L это размах крыла, а здесь оно обозначено как полуразмах. Поэтому величины совпадают. Если крыло представляет собой круг, то формулы также справедливы при подстановке H = L = R, где R – радиус круга. Но у нас контур крыла не описывается аналитической формулой, которую можно так же легко проинтегрировать. Во всяком случае, вид этой формулы нам неизвестен, и нам нужно подобрать необходимое уравнение, описывающее этот контур. Вывод формул Читатели, не знакомые с интегральным и дифференциальным исчислением, могут этот раздел пропустить. Итак, я выбрал кривую Безье, а выражение для квадратичной кривой Безье записывается в параметрической форме так:
Здесь t – параметр, принадлежащий интервалу На самом деле, при параметрической форме задания кривой на плоскости приведенное выше выражение объединяет в себе два уравнения, каждое для своей оси выбранной системы координат. Коэффициенты Начальная и конечная точки у нас имеют следующие координаты:
Координаты средней точки
В дальнейших выкладках нам индексы не понадобятся, так как неизвестная точка всего одна. Поэтому я их пока опущу. Так какую точку выбрать в качестве неизвестной средней опорной точки? Я предположил, что углы стреловидности у корневой и концевой нервюры w и u (Рис. 4) нам известны (замерены на реальном крыле), либо мы их зададим сами, если крыла еще нет. Тогда ее координаты будут координатами точки пересечения касательных к контуру, проведенных из начальной и конечной точек (Рис. 5). Заметьте, что оба угла стреловидности w и u здесь имеют отрицательные значения, поскольку в математике принято за положительное направление отсчета углов считать направление против часовой стрелки.
Рис. 5. К определению координат средней опорной точки Значения этих координат следующие:
Здесь, правда, есть одно ограничение. Если у законцовки кривая контура крыла круто загибается и угол u приближается к девяноста градусам, то tg(u) обратится в бесконечность. Как ни странно, но в этом случае ситуация проще. Надо просто положить z = L. Вторая формула – без изменений. Такой контур крыла с круто загибающейся задней кромкой показан на Рис. 6. Теперь мы можем использовать полученные выражения для вычисления интегралов. Однако в уравнении для Lcax неизвестной является и площадь крыла S, поэтому придется вычислить два интеграла: один для площади, другой для статического момента. Интеграл для площади, при задании кривых в параметрической форме, запишется так:
Здесь
Вычисление таких интегралов трудностей не представляет, это просто трудоемкая рутинная процедура, поэтому выкладки я приводить не буду, чтобы не утомлять читателя. Результирующая формула:
Теперь надо найти Lcax. Формула для вычисления:
Снова длинная рутинная процедура перемножения многочленов и взятие интегралов. Выкладки опускаю, результат таков:
Желающие могут меня перепроверить самостоятельно. Для круто скругленной кромки, в данном случае задней, как на Рис. 6, то есть при z = L, формулы упрощаются.
и
Итак, плечо САХ мы нашли. Но эта величина у нас отсчитывается по оси Z. А теперь надо найти саму САХ, которая у нас измеряется по оси X. Поскольку x у нас задается параметрическим уравнением, то надо найти значение параметра t, которому соответствует Lcax. Подставляя Lcax в уравнение для z(t), и решая его относительно t, получим следующую формулу:
Теперь находим собственно САХ.
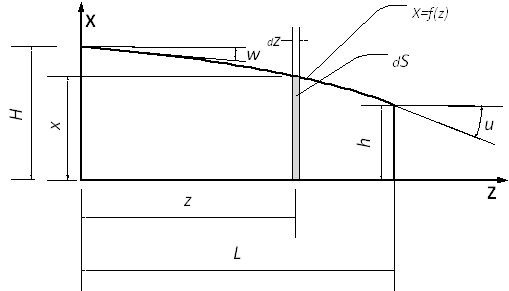
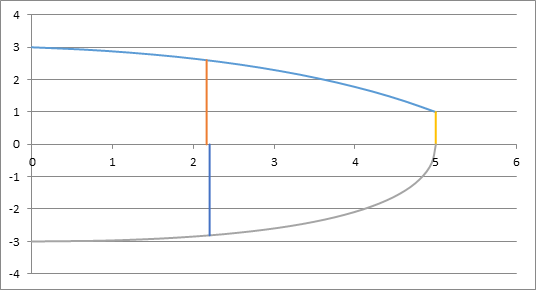
Задача решена! Для получения результата нам понадобились всего четыре формулы. При этом одна из них «попутно» дала нам площадь консоли! Числовой пример Возьмем такое крыло, как на Рис. 5. Исходные данные для него следующие: Полуразмах L = 5 дм; корневая хорда Н = 3 дм; концевая хорда h = 1 дм; угол стреловидности у корневой нервюры w = -3 градуса; угол стреловидности у концевой нервюры u = -45 градусов. Точка пересечения касательных дает те самые координаты третьей опорной точки В нашем случае: Вычислим площадь консоли и Lcax: S = 11,674 кв. дм; Lcax = 2,162 дм. Далее параметр t: tcax = 0,37 И теперь уже собственно CAX = 2,604 дм Положение САХ на графике показано вертикальной линией. Что ж, задачу мы решили. И самое главное, что интегралы мы свели к дробям… А ведь с дробями проще! Но это еще не конец истории. Что если у нас и задняя кромка криволинейная? И если «криволинейность» ее другая? Смотрим на картинку Рис. 6.
Рис. 6. Пример крыла с криволинейными передней и задней кромками Сразу отмечу, что ничего сложного в этой задаче нет. У нас уже есть весь набор инструментов для ее решения. Крыло у нас разбито на две секции: выше оси Z и ниже ее. Я специально выбрал крутое скругление задней кромки, чтобы продемонстрировать возможность оперирования с произвольным контуром крыла. Итак, для верхней (передней) секции крыла мы уже знаем что делать, для нижней (задней) поступаем точно также. Особенность будет заключаться лишь в том, что для нее значения H и h будут отрицательными, поскольку они лежат ниже оси абсцисс, а углы стреловидности положительными. Так что проводим вычисления еще раз с новыми значениями, и получаем параметры для нижней секции крыла. Вот только площадь сегмента получится отрицательной! Конечно, в реальности этого быть не может, это просто мы так «неудачно» выбрали оси координат. Учтем это обстоятельство при вычислении площади консоли. Что делать дальше? Мы имеем две секции, которым присвоим индексы в – для верхней (передней) и н – для нижней (задней). С учетом знаков, суммарная площадь консоли S равна:
Также мы имеем Lcax. Теперь нужно вычислить Lcax для всей консоли по следующей формуле.
Тогда для верхней секции:
Соответственно для нижней:
Здесь опять координата
Пример Продолжим приведенный выше пример (Рис. 6) со следующими значениями исходных величин для нижней секции консоли. Верхняя секция без изменений. Корневая хорда Н = -3 дм; концевая хорда h = 0 дм Угол стреловидности у корневой нервюры w = 0 градусов; у концевой u = 90 градусов. Получим:
И, окончательно: САХ = 5,591 дм На Рис. 6 показаны САХ для верхней и нижней секций консоли. Результирующую САХ я не показал, поскольку она близка к этим двум и на рисунке будет сливаться. Все вычисления удобно проводить в Excel и сразу строить графики контура. Это наглядно покажет, похож ли ваш контур на желаемый, и при случае выявит ошибку в вычислениях. Заключение Обратите внимание, что попутно мы в принципе решили задачку вычисления САХ для многосекционного крыла. Ведь разбиение крыла на участки – это и есть аналог многосекционного крыла, у которого, например, резко меняется контур центроплана, консоли или законцовки. Только угол сопряжения кривых в стыке участков будет разный. Есть и другие особенности в расчете, если секции крыла расположены не вдоль хорды, а вдоль размаха. Далее, необходимо учитывать, что если ваше крыло имеет поперечное V, при этом излом крыла всего один, (верхние конфигурации крыла на плакате Рис. 1), то выведенные выше формулы остаются справедливыми при расчете САХ. Если же крыло имеет два и более излома (нижние конфигурации крыла на плакате Рис. 1), то при расчете САХ придется переходить к проекциям крыла на базовые плоскости. Но подробнее обо всем этом в другой раз… |