| Расчет САХ эллиптического крыла. Разночтения |
| Изготовление авиамоделей - Разработка авиамоделей |
| Автор: Administrator |
|
Юрий Арзуманян (yuri_la) Данная статья является продолжением «трилогии», посвященной расчету Средней Аэродинамической Хорды (САХ) крыла. Она была начата статьей «Расчет САХ крыла с криволинейным контуром» и была продолжена в статье «Расчет САХ. Второе приближение». Затем последовала завершающая, как мне тогда казалось, статья (САХ и геометрия авиамодели). Честно говоря, я считал, что на этом тема исчерпана, и я не собирался к ней больше возвращаться. Однако, в комментариях к первой статье один из участников форума – Сергей Тимофеев (ему спасибо!) обратил внимание на имеющееся расхождение в значениях САХ для эллиптического крыла, которое дано по выведенным мной формулам. Меня это, конечно, «зацепило» и я снова взялся за тему.
Проверив еще раз свои выкладки, я ошибки
не нашел. Более того, я полез на зарубежные сайты для поиска дополнительных
материалов и расчетов. Нашел, что и там есть некоторый разнобой в понимании по
данному вопросу. Вот, например, вывод уравнений для МАС на одном
из
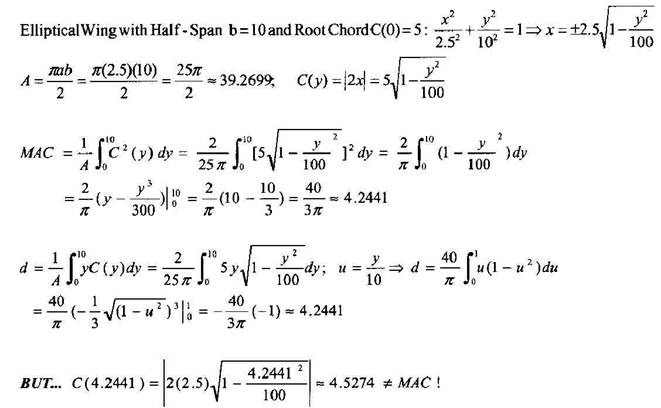
В моих выкладках САХ = 0,905 Н, где Н – корневая хорда. То есть если Н = 5, то 4,5274 от пяти как раз и будет примерно 0,905. Однако Серж Краусс поставил здесь знак неравенства. Почему это? После долгих размышлений я, наконец, понял, в чем заключаются расхождения. Ниже я буду пользоваться теми же обозначениями переменных, которыми пользовался в самой первой статье цикла. Итак, в уравнениях для расчета расстояния до САХ от корневой хорды расхождений нет. Разница только в обозначениях. У меня:
Здесь L – полуразмах крыла. У Сержа:
Полуразмах крыла b у него равен 10-ти, поэтому в пределах интегрирования стоит эта цифра. Поперечная ось системы координат у него обозначена y, у меня z. Соответственно функции: у него C(y), а у меня f(z). A – площадь консоли крыла (у меня обозначена S). Результат интегрирования, разумеется, одинаков. Однако дальше, когда он подставляет полученное значение y в уравнение эллипса, то оказывается, что точка на эллипсе, через которую должна проходить САХ, дает другое, большее значение САХ, чем полученное им по формуле для ее расчета! Вот почему он и поставил знак неравенства. Так в чем же дело? А дело в том, что во всех учебниках и книгах на эту тему используется формула, приведенная, в числе прочего, и в нашем ГОСТ 22833-77. Эта формула в моих обозначениях такова:
Так вот, если вычислить этот интеграл (он, кстати, вычисляется проще – не надо никаких замен переменных), то получится следующее выражение для САХ эллиптического крыла:
А при подстановке Lcax (у Сержа это d) в уравнение эллипса получится:
Итак, в первом случае это приблизительно:
Во втором:
Разница хоть и небольшая, но она есть. Теперь важно показать на рисунке (Рис. 1), как на практике выглядят эти расхождения. Если пользоваться той логикой, которой я руководствовался при написании этих статей, то вопросов и противоречий никаких не возникает. САХ крыла находится на правильном расстоянии от корневой хорды и ограничена контуром крыла (верхний рисунок). Во втором, «официальном» случае, согласно ГОСТ, САХ крыла находится на том же расстоянии от корневой хорды, но «повисает в воздухе», так как не доходит до кромок крыла (нижний рисунок).
Рис. 1. Сравнение результатов расчета САХ эллиптического крыла по различным формулам Как здесь быть, то есть каким расчетом пользоваться, я затрудняюсь рекомендовать. Для меня, например, непонятно от чего отсчитывать положение центра тяжести модели с таким крылом, если пользоваться «официальным» расчетом. Поэтому я оставляю за собой право опираться на собственные расчеты, которые, по моему скромному мнению, не противоречат физическому смыслу САХ, да и в практическом плане не создают неопределенности при определении центровки модели. А каждый моделист, который столкнется на практике с этой дилеммой, должен будет ее разрешить самостоятельно. Важно заметить при этом, что для формы крыла в плане, образованного прямыми линиями (треугольник, трапеция, параллелограмм), результирующие формулы совпадают. |