| Элементы механики полета (продолжение) |
| Обзоры - Теория и практика полетов |
| Автор: Юрий Арзуманян |
|
Часть III Баллистический коэффициент и лобовое сопротивление Первую и вторую часть можно прочитать здесь.
Параметр «баллистический коэффициент», как следует из названия, больше относится к баллистике – науке, которая изучает движение таких тел, как, скажем, пуля, снаряд орудия в канале ствола (внутренняя баллистика) и после его вылета из ствола (внешняя баллистика). Здесь я этот параметр использую исключительно для иллюстрации некоторых сравнительных результатов.
Возьмем для примера два предмета: мяч для настольного тенниса (диаметр 40 мм, масса 2,7 грамма) и стальной шар точно таких же размеров. Его масса будет равна примерно 260 грамм. Коэффициент лобового сопротивления у них одинаковый Сх = 0,5. Площадь миделя Sm = 12,57 кв. см.
Баллистический коэффициент теннисного мяча соответственно равен 0,23 кг/кв. м, а стального шара такого же диаметра почти в сто раз меньше – 0,002442 кг/кв. м.
Какую скорость разовьют оба наших предмета, если будут падать в земной атмосфере с бесконечной высоты? Плотность воздуха равна 1,225 кг/куб. м.
Согласно выведенной выше формуле, теннисный мяч будет парашютировать со скоростью 8,34 м/сек (30 км/ч), а стальной шар со скоростью 80,94 м/сек (291,4 км/ч). Теперь представим, что в атмосфере дует ветер со скоростью 5 м/сек, который сносит оба предмета вбок именно с этой скоростью. (То есть он успел их разогнать до этой скорости за время падения). На какое расстояние вбок их унесет на последних 100 метрах высоты?
Теннисный мяч будет падать 100 метров по вертикали 12 секунд. За это время со скоростью 5 м/сек он пройдет расстояние в горизонтальном направлении 60 метров. А стальной шар будет падать 100 метров по вертикали 1,24 секунды. Он за это время успеет пройти в горизонтальном направлении только 6,2 метра. То есть снос теннисного мяча будет почти в десять раз выше, чем для стального шара.
Это чисто кинематическая иллюстрация влияния веса тела и скорости его движения в атмосфере на устойчивость к ветровому воздействию. То есть мы не учитываем величину силы, действующей на предмет, и заставляющей его отклоняться от прямолинейной траектории. Пример этот, конечно, не слишком показательный для наших целей, по той причине, что мы рассматриваем два предмета сферической формы, для которых аэродинамические характеристики не зависят от ориентации в пространстве. Но я потому и выбрал именно такой пример, чтобы пока не замешивать в рассмотрение влияние других факторов, а именно влияние формы тела. А теперь мы к этому и перейдем.
Рассмотрим теперь более близкий нам пример, а именно горизонтальный полет самолета с постоянной скоростью и воздействие на него бокового ветра. Будем считать, что пилот препятствует самопроизвольному развороту самолета на ветер. То есть он не хочет, чтобы самолет стал лететь строго против ветра, а с помощью руля направления удерживает его на желаемом курсе. Это означает, что самолет летит с некоторым углом скольжения (угол между проекцией продольной оси самолета на горизонтальную плоскость и проекцией вектора скорости полета на ту же плоскость). Проще говоря, самолет летит как-бы немного боком, чтобы бороться со сносящим его ветром.
Рассмотрим, какова будет разница в устойчивости самолета к ветру, если он летит с разной скоростью. Положим, что скорость ветра, как и в предыдущем примере, равна 5 м/сек, а самолет в первом случае летит с относительной скоростью 10 м/сек (36 км/ч), а во втором – 20 м/сек (72 км/ч). Здесь под относительной скоростью понимается скорость модели относительно атмосферы. Ее еще называют воздушной скоростью. Но обычно самолету надо прилететь из пункта А в пункт Б, которые находятся на земле. При этом, как мы знаем, при сильном встречном ветре можно сделать так, что модель будет висеть в воздухе неподвижно. То есть скорость относительно воздуха есть, а относительно земли – нет. Поэтому говорят еще о земной скорости.
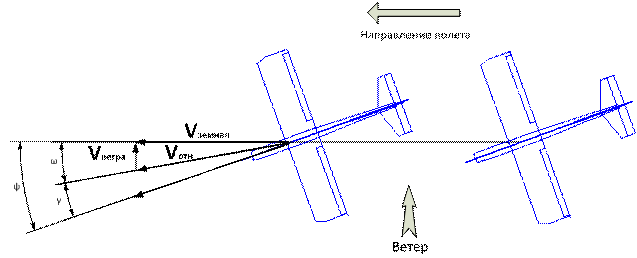
Смотрим на рисунок.
На этом рисунке угол ? называется углом рыскания. А угол ? называется углом скольжения. О нем мы и говорили выше. Этот угол является аналогом угла атаки ?, только угол атаки измеряется в вертикальной плоскости, а этот угол – в горизонтальной. Аналогом угла ? в вертикальной плоскости является угол тангажа ?. Угол, который я здесь произвольно обозначил символом ?, в динамике полета обычно не рассматривается, а вот штурман самолета, которому надо прокладывать курс, вполне вероятно его использует.
Для нашего примера этот угол вычисляется через синус отношения Vветра к Vотн. В первом случае он равен 30 град., а во втором 14,5 град. Чтобы определить боковую силу, действующую на модель, надо иметь данные о ее аэродинамических характеристиках, тяге, угле скольжения и т.п. Однако мы знаем, что эта сила прямо пропорциональна углу скольжения ? (если величина этого угла не слишком велика), скоростному напору и площади миделя. (Обычно все аэродинамические коэффициенты: лобового сопротивления, подъемной и боковой силы, относят к одной площади – площади миделя.)
Поэтому мы можем с полным основанием предположить, что если угол ? уменьшится более чем в два раза с увеличением скорости полета вдвое, то и угол скольжения ? также сильно уменьшится. А это означает, что модель будет менее повернута боком к набегающему потоку, то есть как-бы уменьшится «парусность» модели, и ее будет существенно меньше сносить ветром!
Итак, мы установили, что на устойчивость модели к ветровому сносу в положительную сторону влияют увеличение веса модели (масса), лучшая обтекаемость, малая площадь боковой проекции и высокая скорость полета. Продолжение следует… Ю. Арзуманян yuri_la |