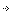| Винты для мультироторных систем |
| Обзоры - Теория и практика полетов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Автор: Administrator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ю. Арзуманян (yuri_la)
Периодически мне мои друзья-моделисты задают вопросы, относящиеся к подбору оптимального воздушного винта для своих моделей, и в особенности по данной теме. Сразу хочу оговориться, что сами по себе мультироторные системы (далее я буду использовать термин «мультикоптеры») мне не интересны, в моем авиапарке их нет, и пока не предвидятся. Я их не строил и не занимался их анализом. Поэтому для меня эта тема представляет чисто теоретический интерес, и, конечно, желание помочь товарищам играет не последнюю роль. Я также надеюсь, что статья окажется полезной и всем ее читателям. Поэтому и взялся за перо.
В моих обсуждениях данной темы с друзьями я всегда указывал на то, что мультикоптер – сложный летательный аппарат, оптимизация параметров которого должна проводиться в комплексе. То есть нельзя по отдельности оптимизировать винты, электромоторы, батарейки, конструкцию. Ведь, скажем, увеличение диаметра винтов может повлечь необходимость установки более мощных моторов (помимо увеличения веса собственно винтов), что приведет к росту потребляемой мощности, соответственно потребует более емких, значит более тяжелых батарей и т.д. Все это скажется на взлетном весе мультикоптера и, в конечном счете, повлечет либо снижение веса полезной нагрузки, либо уменьшение полетного времени.
Однако тема комплексной оптимизации достаточно обширна, и охватить ее в одной статье сложно. Поэтому задача данной статьи – установление направлений оптимизации и вывод неких зависимостей применительно конкретно к параметрам винтов, которые могут быть положены в основу комплексной оптимизации.
Хочу напомнить, что некоторое обсуждение вопросов подбора параметров воздушного винта проводилось в этой теме. Правда, там речь шла о скоростной маневренной модели самолета, а режимы работы винта мультикоптера имеют свои отличия. Они гораздо ближе к режиму работы с малой относительной поступью винта или вообще нулевой (статическая тяга), характерному для режима висения. Эта особенность в какой-то степени упрощает задачу, но не слишком.
Чтобы не ссылаться все время на упомянутую тему, повторю здесь основные зависимости, характеризующие работу воздушного винта, которыми нам придется оперировать. Итак, относительная поступь винта:
Тяга:
Потребляемая мощность:
КПД винта:
Здесь и далее будут использованы следующие обозначения:
n – число оборотов винта D – диаметр винта
Из известных зависимостей для КПД винта (см. график) видно, что максимум его КПД достигается, когда относительная поступь численно примерно равна трем четвертям его относительного шага
Рис. 1. Примерная зависимость КПД винта от относительной поступи
К сожалению, для мультикоптера работа винта с максимальным КПД практически неосуществима по той причине, что вертикальная скорость таких аппаратов относительно мала, а в режиме висения она и вовсе равна нулю. В то же время для мультикоптера, используемого как съемочная платформа, режим висения или перемещения с малой горизонтальной скоростью на одной высоте, что практически эквивалентно, является одним из основных. Поэтому при
При этом возникает кажущийся парадокс, так как получается, что затрачиваемая на вращение воздушного винта энергия расходуется впустую. На самом деле это методическая условность, так как в действительности для такого режима полета винт производит полезную работу по отбрасыванию назад воздушной массы, то есть создает тягу, что и удерживает аппарат на заданной высоте. Как это можно вывести математически, показано ниже.
Для наглядности стоит отвлечься от нюансов и сложностей газовой динамики, а ограничиться только методами классической механики. Тогда можно получить выражение для тяги винта в некотором идеализированном примере. Привожу его здесь для того, чтобы показать возможный способ получения представленных выше выражений для тяги винта и потребной мощности для его вращения.
Из элементарной механики нам известно выражение импульса, или по-другому количества движения:
Здесь
Продифференцируем по времени это выражение. Получим:
Нас интересует в данном случае как раз сила
Здесь
Чтобы каким-то образом получить входящие в формулу значения, целесообразно рассмотреть некое идеальное устройство, для чего как нельзя лучше подходит так называемый
В быту это устройство называется просто шнек. И он, например, используется в такой штуке, как обыкновенная мясорубка. Только мы, как сказано, рассмотрим идеальное устройство, которое перемещает (отбрасывает, подобно импеллеру) воздух. При этом нет ни зазоров, утечек, трения, вязкости и сжимаемости воздуха, ни прочих явлений, связанных с реальной газодинамикой.
Итак, если такой винт-шнек из бесконечно тонкого материала вращается в цилиндрической трубе с постоянной скоростью, то скорость отбрасываемого им воздуха на выходе из нее постоянна по времени. Тогда ускорение массы обращается в ноль и в правой части формулы останется только одно слагаемое:
Рассмотрим это слагаемое. Масса воздуха, заключенная в одном витке шнека, равна
А эта величина, помноженная на число оборотов винта в единицу времени, как раз и даст нам искомый расход массы
Теперь надо определиться со скоростью отброса массы. Так как масса воздуха, заключенная в одном витке винта-шнека перемещается им за один оборот на величину его шага, то помножив шаг винта на число оборотов
И тогда:
Итак, мы получили тягу, создаваемую идеальным винтом Архимеда. Теперь несколько преобразуем полученную формулу. Введем в нее использованный нами ранее относительный шаг винта
Если теперь сравнить полученное выражение с известным из учебников выражением для тяги воздушного винта, приведенным выше, то мы увидим много общего. Обозначим коэффициентом
Тогда два выражения для тяги будут выглядеть так:
и
Как видите, два выражения удивительно похожи, и отличаются только коэффициентами
Важно отметить, что тяга винта зависит от его диаметра в четвертой степени. При этом не стоит забывать, однако, что потребляемая винтом мощность также зависит от диаметра винта, только уже в пятой степени! Кстати, вывести формулу для потребной мощности также несложно. Достаточно вспомнить, что работа есть сила, помноженная на пройденный путь, а мощность это работа в единицу времени. Таким образом, потребляемая мощность получится, если силу
Теперь мы можем перейти к рассмотрению параметров реального винта и попытаться понять, с учетом сделанных замечаний, направление поиска оптимума этих параметров применительно к мультикоптеру. Тут возможны два подхода к решению данной задачи. Первый – это проектировать оптимальный винт «с нуля», исходя из набора неких критериев, и второй – подбирать готовый винт из имеющихся в продаже. Разумеется, первый подход вряд ли приемлем для рядового моделиста, поэтому этим мы заниматься не будем. Будем подбирать готовый винт. Однако для понимания того, в каком направлении двигаться, надо коротко сказать о классических методах проектирования воздушных винтов.
Итак, обычно лопасть винта рассматривается по аналогии с крылом, как некая несущая плоскость, движущаяся в потоке с определенным углом атаки. Сама лопасть разбивается по ее длине на участки (секции), имеющие определенный аэродинамический профиль. Профиль может быть одинаковым по всей длине лопасти, или переменным, что в нашем случае несущественно. Каждая секция лопасти представляется элементом, создающим подъемную силу и лобовое сопротивление. Последнее создает момент, препятствующий вращению, на который и расходуется мощность мотора. Суммируя по всем секциям лопасти, и помножив на число лопастей, получается тяга, создаваемая винтом и момент сопротивления вращению винта.
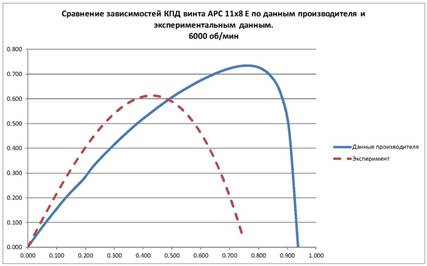
Поскольку угол атаки элемента лопасти зависит от скорости набегающего потока, частоты вращения винта и угла установки этого элемента, то максимум тяги при минимуме сопротивления получается при таком режиме, при котором аэродинамическое качество лопасти максимально. Если теперь взглянуть на поляру типичного аэродинамического профиля, который используется в лопасти винта, например, как на Рис. 2 ниже, то можно увидеть, что максимальное качество профиля достигается на достаточно малых углах атаки (точка, где угол наклона касательной к поляре максимален).
Рис. 2. Типичная поляра профиля
На других режимах работы винта угол атаки не соответствует максимальному качеству. Именно поэтому кривая КПД винта имеет ярко выраженный горб, как видно из Рис. 1. Таким образом, для каждого винта имеется оптимальный режим полета, на который он рассчитан. В других условиях приходится жертвовать эффективностью работы винта в угоду расширения диапазона доступных полетных режимов. В этом смысле мультикоптер, который используется как съемочная платформа, является практически однорежимным летательным аппаратом. Те же аппараты, которые умеют «кувыркаться» в воздухе и выполнять всякие энергичные полетные маневры, к таковым отнесены быть не могут. Поскольку первые, как мне кажется, более распространены, я именно на них и сделаю акцент и буду рассматривать режим висения и перемещения с малой горизонтальной скоростью как основной.
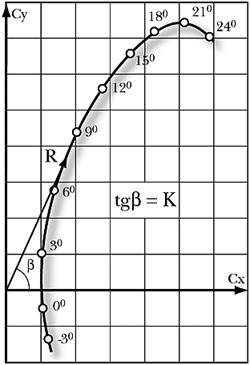
Обратимся теперь к Рис. 3. Что здесь для нас важно, так это то, что эффективная работа элемента лопасти винта зависит, помимо всего прочего, от угла установки этого элемента. Последний же определяется геометрическим шагом винта, который мы и собираемся выбирать наряду с диаметром винта.
Рис. 3. Угол атаки элемента лопасти винта
Обращаю ваше внимание на то, что для режима статической тяги скорость набегающего потока близка к нулю (вектор V на рисунке), так как она определяется только скоростью подсоса воздуха в плоскость вращения винта из внешней невозмущенной среды. В этом случае угол атаки элемента лопасти будет очень близок к углу установки этого элемента. Для классического винта постоянного шага этот угол достаточно велик у ступицы винта и плавно уменьшается по длине лопасти. А поскольку максимальное качество элемента лопасти, как сказано, достигается при малых углах атаки, то получается, что эффективно работает только периферийная часть лопасти. Значит, при таком режиме работы винта желательно, чтобы вся лопасть была сформирована с одним малым более-менее постоянным по всему размаху углом установки.
С другой стороны, малый угол атаки лопасти даст малую скорость отбрасываемого потока, то есть малую тягу, как мы видим из выведенной выше формулы, где тяга есть произведение расхода массы на отбрасываемую скорость. Чтобы эту скорость увеличить, есть два пути. Можно удлинять лопасть, так как линейная скорость движения элемента лопасти при постоянной скорости вращения тем больше, чем дальше он от оси вращения. Второй путь – это увеличение частоты вращения винта (числа оборотов).
Первый путь – длинная лопасть с малым углом установки (малым шагом) должна нам что-то напоминать… Ну, конечно! Это же лопасть ротора вертолета! То есть, двигаясь по этому пути, мы придем к тому, к чему вертолетчики давно уже пришли. Проблема, однако, в том, что для мультикоптера на диаметр винта наложены геометрические ограничения из-за размеров аппарата. Лопасти соседних винтов не должны цеплять друг друга. Более того, взаимодействие близко расположенных завихренных потоков от соседних винтов также нежелательно. Между ними должно быть достаточное расстояние, соизмеримое с диаметром единичного винта. То есть для мультикоптера на диаметр винта наложено ограничение сверху. Поэтому двигаться в направлении использования винтов большего диаметра можно лишь до определенного предела. Остаются другие возможности, о чем пойдет речь ниже, когда мы перейдем к конкретным примерам.
Поскольку для мультикоптера в режиме висения легко определить потребную статическую тягу, так как она должна быть равна весу аппарата, то тягу единичного винта можно получить, просто поделив вес аппарата на коэффициент k, который я назову «мультипликатором» по аналогии с термином «мультикоптер». То есть для трикоптера k = 3, для квадрокоптера k = 4 и т.д. Тогда при известной тяге подбор параметров винта можно свести к нахождению минимальной потребляемой мощности для приведения его во вращение. Используя имеющиеся выражения для тяги и мощности, исключив из рассмотрения число оборотов
Из этого выражения уже следует, что потребляемая мощность будет тем меньше, чем больше диаметр винта, что подтверждает ранее сделанные заключения. Если задаться некоторым диапазоном потребной тяги и вычислить для каждого значения тяги потребляемую мощность, то можно построить графики сравнительных данных по нескольким выбранным нами винтам для определения наилучшего. Однако для того чтобы проделать такую работу необходимы либо данные экспериментов для получения значений коэффициентов тяги и мощности, либо, если таковые имеются, данные производителя винтов. Поскольку экспериментальных данных у нас нет, остается второе. С этим, к сожалению, тоже не густо. Такие данные мне известны только для винтов марки АРС. Их можно найти сайте производителя
В таблицах расчетных данных, приведенных по этой ссылке, я выбрал для сравнения четыре винта, которые имеют маркировку MR (multi rotor). То есть они предназначены как раз для мультироторных систем. Какие это винты – показано на графике ниже. Для каждого винта приведены таблицы расчетных данных для разного числа оборотов. Из этих таблиц надо выбрать только первые строчки, когда V = 0, J = 0, что соответствует режиму статической тяги. Тогда для винта 10х4.5 MR, например, получится вот такая таблица:
Таблица 1. Расчетные данные параметров винта 10х4.5 MR
Аналогичным образом преобразованы таблицы и по трем остальным винтам. Я ограничился числом оборотов 15000 об/мин, считая, что для получения качественной картины этого достаточно. Мощность и тяга уже приведены, поэтому считать по формуле выше ничего не надо. Я только перевел мощность в л.с. и тягу в фунтах в килограммы и ватты. По правде говоря, самим величинам тяги и мощности я не верю. Выше я уже давал графики расчетных и экспериментальных значений (Рис. 1). Однако для сравнительного анализа ими пользоваться можно, так как расчеты проведены по одной методике.
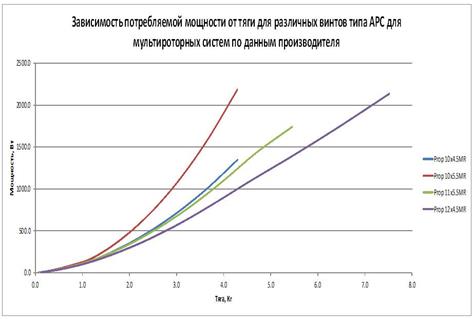
Получившиеся сравнительные результаты видны на Рис. 4.
Рис. 4
Как видите, наши теоретические выкладки графиком подтверждаются. Потребляемая мощность ниже для винтов с меньшим шагом и большим диаметром.
В заключение я только должен еще раз повторить, что всего лишь частный результат. Я не учитывал различие в весе винтов и влияние многих других факторов, на которые я обращал внимание в начале статьи. Но при прочих равных условиях выводы, касающиеся диаметра и шага винта, справедливы. Конечно, хорошо бы провести более полную, комплексную оптимизацию. Но это уже тема другой статьи… |