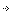| Расчет тросовых приводов рулей |
| Изготовление авиамоделей - Разработка авиамоделей |
| Автор: Administrator |
|
Тросовый привод аэродинамических рулей радиоуправляемых моделей
Юрий Арзуманян (yuri_la)
Тросовая система управления рулями применялась еще на заре авиации, а в радиоуправляемых моделях сегодня довольно часто используется на относительно больших моделях. При этом такая система, как правило, применяется в приводе руля направления.
Достоинством такой системы является малый вес при передаче усилия на приличное расстояние и удачная развесовка, особенно для пилотажных 3D моделей. Хотя для них идеальным было бы использование сервомашинок в хвосте с жесткими короткими тягами для точного управления, но это сопряжено с дополнительными массами в хвосте модели, так как мощные сервомашинки весят немало и к ним еще надо тянуть сервоудлинители, которые, вероятно, весят не меньше чем тросы. Отсюда возможные проблемы с центровкой, увеличение моментов инерции модели, что нежелательно для энергичного пилотажа.
Тросовая система управления этих недостатков лишена, но ей присущи другие, такие как провисание ведомого троса в некоторых схемах, что при перекладке руля означает запаздывание на срабатывание (мертвая зона) и рывок после того, как провис будет выбран.
Из этого возникает необходимость анализа геометрии системы для ее правильной организации, определения соотношений размеров качалок и кабанчиков, и т.п. для минимизации влияния недостатков на эффективное и точное управление моделью. Этим и займемся.
Рассматривать будем тросовый привод руля направления (РН). Принципиально схемы управления возможны три. Условно назовем их «крест», когда тросы перекрещиваются, «трапеция», когда тросы не перекрещиваются, но плечи качалок и кабанчиков не равны. Третья схема – «параллелограмм», когда тросы не перекрещиваются, смещения точек подвеса троса нет, а плечи качалок и кабанчиков равны, рассматриваться не будет, так как там нечего рассматривать в плане геометрии. В ней провисание тросов отсутствует, но угол отклонения руля будет в точности равен углу поворота качалки серво, в то время как в двух других схемах можно за счет соотношения плеч добиться «повышающей передачи». Притом схема «трапеция» сводится к схеме «параллелограмм» при задании нулевых смещений и равных плеч качалки и кабанчика.
Часть I. Схема «крест»
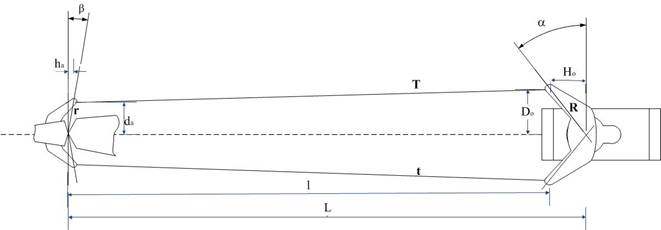
Мне представляется, что схема «крест» наиболее распространена, во всяком случае, на нескольких моих покупных моделях применена только такая схема и это сделано согласно инструкциям по сборке. Поэтому рассмотрение начнем именно с нее. Геометрия системы представлена на Рис. 1.
Рис. 1. Геометрия системы «крест» в нейтральном положении
Будем считать, что нам заданы следующие величины (обозначения на Рис. 1): L – расстояние между осями качалки серво и подвеса РН R – плечо качалки серво r – плечо кабанчика РН
Можно задать вместо углов линейные смещения точек подвеса (в прилагаемом Excel-файле такая возможность предусмотрена). Но так как мы будем далее оперировать угловыми перемещениями качалки и кабанчиков, то задание смещений в угловой мере удобнее в расчетах. А линейные смещения вычисляются по простым формулам:
Приведенные плечи качалки и кабанчика D и d вычисляются соответственно:
Расстояние между точками подвеса тросов вдоль продольной оси модели l:
Длина троса T нам неизвестна. Вычислить ее несложно. Рассмотрим трос, идущий от верхнего на рисунке плеча качалки. Назовем его ведущим тросом. Он будет тянуть нижний кабанчик на рисунке, и отклонять РН. Второй трос мы назовем ведомым, так как трос не передает толкающего усилия. Нас интересует, будет ли он провисать? И если да, то как это явление устранить, или хотя бы минимизировать?
Для вычисления Т достаточно мысленно сместить ведущий трос параллельно самому себе вверх на величину d. Тогда получится прямоугольный треугольник, у которого Т является гипотенузой. Отсюда:
Теперь все нужные нам величины в нейтральном положении системы известны. Рассмотрим поворот качалки серво по часовой стрелке на некоторый угол ?. Ведущий трос потянет кабанчик и повернет его и соответственно РН на некоторый угол ?, который нам и предстоит определить. Это показано на Рис. 2.
Рис. 2. Геометрия системы «крест» при отклонении РН
Варьируя углом ?, мы сможем получить зависимость угла поворота РН от угла поворота качалки серво. Далее, вычисляя теоретическую длину ведомого троса t, мы сможем увидеть отличается ли она от реальной Т, то есть, имеет ли место провисание ведомого троса и каково оно. Сразу отметим, что если при определенном сочетании исходных данных вместо провисания ведомого троса при повороте качалки серво имеет место его натяжение, то это означает, что натягиваются сразу оба троса. Это ставит работоспособность схемы под вопрос. Особенно это характерно для схемы со значительными смещениями точек подвеса тросов на качалке и кабанчике.
Процесс вычислений начнем с определения новых значений D и Н.
Новые значения d и h нам пока неизвестны.
Выразим h через d:
И обозначим:
Тогда
По аналогии с (*) можно записать
Имеем одно уравнение с одним неизвестным d, которое сводится к стандартному квадратному уравнению. Уравнение дает два решения, оба теоретически возможны, но из них нас интересует только одно, которое выбрано из реальной кинематики системы.
Следует отметить, что в особом вырожденном случае два решения сводятся к одному. Это произойдет при повороте качалки на такой угол, при котором подкоренное выражение обратится в ноль. Геометрически это будет означать, что трос ориентирован вдоль линии, проходящей через ось вращения РН и дальнейший поворот РН невозможен. Это еще одно ограничение в дополнение к тому, о котором речь шла выше.
В формуле приняты следующие обозначения:
Теперь можно определить угол поворота РН ? из следующего выражения:
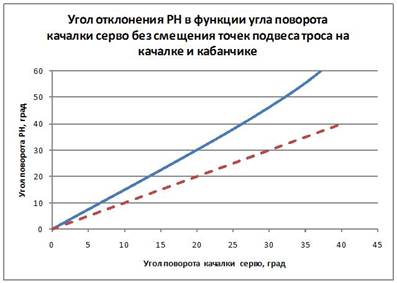
Связь между углами ? и ? очевидно будет нелинейной, как мы увидим далее из графиков, и степень этой нелинейности будет зависеть от соотношений плеч качалки и кабанчика, а также от смещений точек подвеса тросов. Вот, например, как ведет себя угол отклонения РН в функции угла поворота качалки серво (Рис. 3) при нулевых смещениях точек подвеса тросов (
Рис. 3
Как видно из графика, угол отклонения РН больше угла поворота качалки, то есть имеет место та самая «повышающая передача».
Теперь осталось найти решение для определения величины провисания ведомого троса. Для этого мы воспользуемся уже разработанным нами алгоритмом по вычислению длины ведущего троса Т, только для ведомого троса его теоретическая длина t вычисляется для значений угла ? с минусом. То есть:
И по аналогии с (*)
Провисание троса в виде разницы его фактической длины и ее теоретического значения:
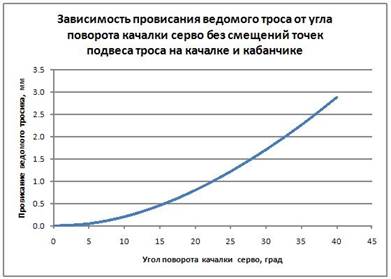
Для тех же исходных данных, что и в вышеприведенном примере, имеем следующую картинку для провисания ведомого троса (Рис. 4).
Рис. 4
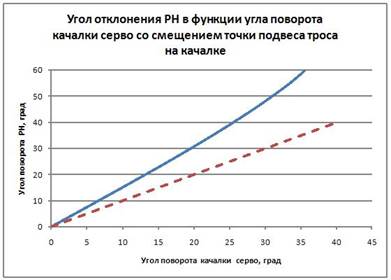
Как видно из рисунка, провисание троса достигает нескольких миллиметров. Посмотрим, что будет, если мы зададим начальные смещения точек подвеса тросов. Скажем, мы используем качалку с углом смещения 7 градусов. Это соответствует линейному смещению в 5,5 мм. Кабанчики оставим прежние, то есть с нулевым смещением. Для этого случая имеем следующие картинки. Вот угол поворота РН (Рис. 5).
Рис. 5
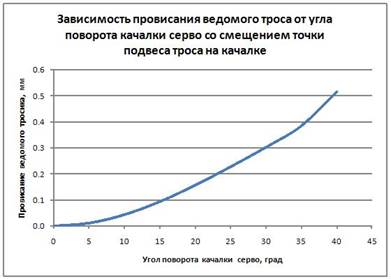
Как видите, картинка почти не поменялась. Что касается провисания ведомого троса, то картина следующая (Рис. 6).
Рис. 6
Провисание троса осталось, но оно уже меньше почти в 6 раз! Следовательно, есть повод поварьировать исходными данными для получения наилучшего результата. Только помните о предупреждениях, данных в начале статьи.
Дальнейший анализ можно продолжать самостоятельно, так как решение задачи запрограммировано в Excel. Файл находится
Часть II. Схема «трапеция»
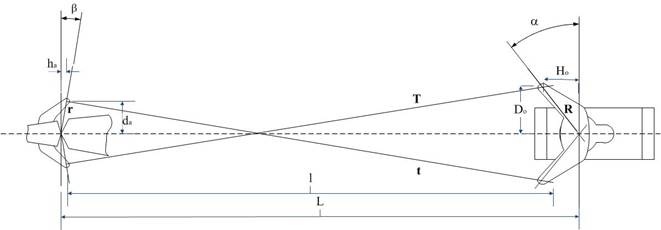
Геометрия системы представлена на Рис. 7.
Рис. 7. Геометрия системы «трапеция» в нейтральном положении
Обозначения переменных оставим прежними. По аналогии со схемой «крест» смещения:
Приведенные плечи качалки и кабанчика:
Расстояние между точками подвеса тросов вдоль продольной оси модели l:
Длину троса T также несложно вычислить.
Аналогично предыдущей схеме рассмотрим поворот качалки серво по часовой стрелке на некоторый угол ?. Ведущий трос потянет кабанчик и повернет его и соответственно РН на некоторый угол ?, который нам и предстоит определить. Здесь РН поворачивается в ту же сторону, что и качалка, по часовой стрелке.
Как и ранее:
Снова выразим h через d:
И обозначим:
Тогда
И также по аналогии с (**) можно записать
Здесь решение отличается от предыдущего только знаками:
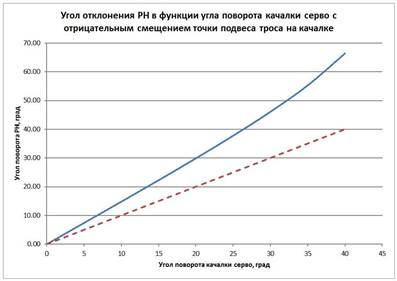
Программа для вычислений находится в том же файле, ссылка на который дана выше. Я не буду здесь анализировать много вариантов исполнения данной схемы. Отмечу только, что при нулевых начальных смещениях точек подвеса троса схема сразу получается с натяжением обоих тросов. А вот если качалку серво перевернуть зеркально, то есть задать на ней отрицательное начальной смещение, то получим такие характеристики:
Рис. 8
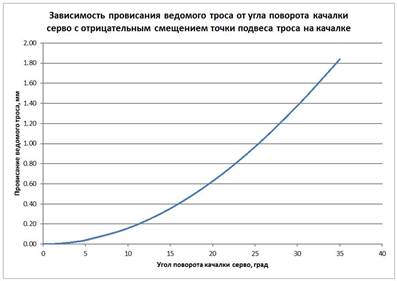
Здесь также имеет место «повышающая передача». А вот что происходит с провисанием ведомого троса (Рис. 9).
Рис. 9
В этой схеме провисание меньше, чем в схеме «крест» с нулевыми смещениями точек подвеса троса (см. Рис. 4), однако больше чем в схеме с положительным смещением точек подвеса троса на качалке (Рис. 6).
Таким образом, инструмент для анализа двух схем «крест» и «трапеция» разработан, желающие могут экспериментировать с ними самостоятельно.
Приложение: Файл Excel для расчетов.
Данная статья в формате PDF находится |